题目内容
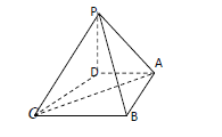
【题目】已知棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 和
和![]() 的中点.
的中点.
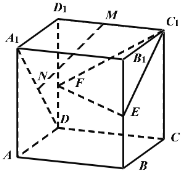
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证法一:连结![]() 交
交![]() 于点
于点![]() ,利用平几知识证四边形
,利用平几知识证四边形![]() 为平行四边形,再根据线面平行判定定理得结果;证法二:取
为平行四边形,再根据线面平行判定定理得结果;证法二:取![]() 中点
中点![]() ,利用平几知识证
,利用平几知识证![]() ∥
∥![]()
![]() ,再根据线面平行判定定理得结果;
,再根据线面平行判定定理得结果;
(2))解法一与解法二,利用等体积法求点到直线距离.
(1)证法一:如图连结![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 为
为![]() 的中点,连结
的中点,连结![]() ,
,![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 为
为![]() 的中位线,∴
的中位线,∴![]() ∥
∥![]() ,
,![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ∥
∥![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形
为平行四边形
∴![]() ∥
∥![]() ,∵
,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ∥平面
∥平面![]() .
.
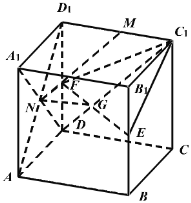
证法二:如图取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,因为正方体
,因为正方体![]() ,
,
![]() 分别为
分别为![]() 中点,所以可得四边形
中点,所以可得四边形![]() 和四边形
和四边形![]() 均为平行四边
均为平行四边
形,所以![]() ∥
∥![]() ∥
∥![]() ,所以平面
,所以平面![]() 即为平行四边形
即为平行四边形![]() 所在平面,因为
所在平面,因为![]()
为![]() 的中点,所以也为
的中点,所以也为![]() 中点,且
中点,且![]() 为
为![]() 中点,所以
中点,所以![]() ∥
∥![]()
![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.

(2)解法一:延长![]() 到点
到点![]() ,使得
,使得![]() ,连结
,连结![]() ,则
,则![]() ∥平面
∥平面![]() ,
,
则![]() 到平面
到平面![]() 的距离即
的距离即![]() 到平面
到平面![]() 的距离,
的距离,![]() ,点
,点![]() 到平面
到平面![]() 的距
的距
离为![]() ,
,![]() ,
,

设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,即
,即![]()
可得![]() ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]()
解法二:由证法二知点![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 的距离,所以
的距离,所以![]() ,
,
且![]() ,
,![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为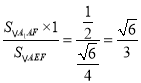 .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目