题目内容

在△ABC中，2
AE
=3
EC
，
BD
=
1
3
BC
，且
AD
、
BE
交于点F，试用向量的方法求|
AF
|：|
FD
|．
考点：向量数乘的运算及其几何意义
专题：平面向量及应用
分析：画出图形，结合图形，设
AB
=
a
，
AC
=
b
，由A、D、F三点共线，B、E、F三点共线，求出
AF
与
AD
的关系，即得|
AF
|：|
FD
|的值．
解答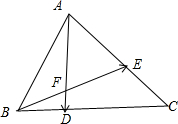： 解：画出图形，如图所示，
设
AB
=
a
，
AC
=
b
，
∴
AE
=
3
5
b
，
CD
=
2
3
CB
=
2
3
（
AB
-
AC
）=
2
3
a
-
2
3
b
；
∴
BE
=
AE
-
AB
=
3
5
b
-
a
，
又A、D、F三点共线，
∴
AF
=m
AD
=m（
AC
+
CD
）=m（
b
+
2
3
a
-
2
3
b
）=
2
3
m
a
+
1
3
m
b
，
B、E、F三点共线，
∴
BF
=n
BE
，
即
AF
-
AB
=n（
AE
-
AB
），
∴
AF
=
AB
+n
AE
-n
AB
=（1-n）
a
+
3
5
n
b
；
∴
2
3
m=1-n
1
3
m=
3
5
n
，
解得m=
9
11
，n=
5
11
；
∴
AF
=
9
11
AD
，即|
AF
|=
9
11
|
AD
|；
∴|
AF
|：|
FD
|=9：2．
点评：本题考查了平面向量的线性表示的应用问题，解题时应灵活应用平面向量的线性表示，是中档题．
练习册系列答案
相关题目
在西部大开发中，某市的投资环境不断改善，综合竞争力不断提高，今年一季度先后有甲、乙、丙三个国际投资考察团来到该市，独立地对A，B，C，D四个项目的投资环境进行考察．若甲考察团对项目A满意且对项目B，C，D三个中至少有1个项目满意，则决定到该市投资；否则，就放弃到该市投资．假设甲考察团对A，B，C，D四个项目的考察互不影响，且对这四个项目考察满意的概率分别如下：
（1）求甲考察团决定到该市投资的概率；
（2）假设乙、丙考察团决定到该市投资的概率都与甲相等，记甲、乙、丙三个考察团中决定到该市投资的考察团个数为随机变量ξ，求ξ的分布列和期望．
考察项目ABCD
满意的概率
5
7
2
3
1
2
3
5
关于下列命题：
①若函数y=2x的定义域是{x|x≤0}，则它的值域是{y|y≤1}；
②若函数y=
1
x
的定义域是{x|x＞2}，则它的值域是{y|y≤
1
2
}；
③若函数y=x2的定义域是{x|-2≤x≤2}，则它的值域是{y|0≤y≤4}；
④若函数y=log2x的定义域是{y|y≤3}，则它的值域是{x|0＜x≤8}；
其中不正确的命题序号是
 
．（注：把你认为不正确的命题的序号都填上．）
已知an=
3
2n-101
（n∈N*），数列{an}的前项和为Sn，则使Sn＞0的n最小值（　　）
A、99B、100
C、101D、102
函数f（x）=lgx+x的零点所在的区间为（　　）
A、（
1
10
，
1
2
）
B、（0，
1
10
）
C、（
1
2
，1）
D、（1，2）
设函数f（x）=
x2+x+1
x2+1
在x＞0时最大值为M，x＜0时最小值为m，则M+m=
 
．
已知，椭圆C过点A（1，
3
2
），两个焦点为（-1，0），（1，0）
（1）求椭圆C的方程；
（2）E，F是椭圆C上的两个动点，如果只想AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．
已知A，B两地相距800m，在A地听到炮弹爆炸声比在B地晚2s，且声速为340m/s，求炮弹爆炸点的轨迹方程．
设函数f（x）=
x+2
x+1
，用单调性定义证明f（x）在（-1，+∞）上是减函数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网