题目内容
【题目】某班在一次个人投篮比赛中，记录了在规定时间内投进
个球的人数分布情况：
进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
投进 | 1 | 2 | 7 | 2 |
其中
和
对应的数据不小心丢失了，已知进球3个或3个以上，人均投进4个球；进球5个或5个以下，人均投进2.5个球．
（1）投进3个球和4个球的分别有多少人？
（2）从进球数为3，4，5的所有人中任取2人，求这2人进球数之和为8的概率．
【答案】（1）投进3个球和4个球的分别有2人和2人；（2）
.
【解析】
（1）设投进3个球和4个球的分别有
，
人，则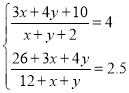
,解方程组即得解.（2）利用古典概型的概率求这2人进球数之和为8的概率．
解：（1）设投进3个球和4个球的分别有，人，则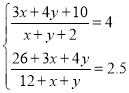
解得
．
故投进3个球和4个球的分别有2人和2人．
（2）若要使进球数之和为8，则1人投进3球，另1人投进5球或2人都各投进4球．
记投进3球的2人为
，
；投进4球的2人为
，
；投进5球的2人为
，
．
则从这6人中任选2人的所有可能事件为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
．共15种．
其中进球数之和为8的是，，，，，有5种．
所以这2人进球数之和为8的概率为
．
【题目】
年底某购物网站为了解会员对售后服务（包括退货、换货、维修等）的满意度，从
年下半年的会员中随机调查了
个会员，得到会员对售后服务的满意度评分如下：
根据会员满意度评分，将会员的满意度从低到高分为三个等级：
满意度评分 | 低于 |
| 不低于 |
满意度等级 | 不满意 | 比较满意 | 非常满意 |
（1）根据这
个会员的评分，估算该购物网站会员对售后服务比较满意和非常满意的频率；
（2）以（1）中的频率作为概率，假设每个会员的评价结果相互独立.
（i）若从下半年的所有会员中随机选取
个会员，求恰好一个评分比较满意，另一个评分非常满意的概率；
（ii）若从下半年的所有会员中随机选取
个会员，记评分非常满意的会员的个数为
，求
的分布列，数学期望
及方差
.
