题目内容
11.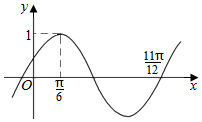 函数$f(x)=Asin(ωx+φ)\;(A>0\;,\;ω>0\;,\;|φ|<\frac{π}{2})$的部分图象如图所示,则将y=f(x)的图象向右平移$\frac{π}{6}$个单位后,得到的函数图象的解析式为( )
函数$f(x)=Asin(ωx+φ)\;(A>0\;,\;ω>0\;,\;|φ|<\frac{π}{2})$的部分图象如图所示,则将y=f(x)的图象向右平移$\frac{π}{6}$个单位后,得到的函数图象的解析式为( )| A. | y=sin2x | B. | $y=sin(2x+\frac{2π}{3})$ | C. | $y=sin(2x-\frac{π}{6})$ | D. | y=cos2x |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.再根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由函数的图象可得A=1,$\frac{3}{4}$T=$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{11π}{12}$-$\frac{π}{6}$,
∴ω=2.
再根据五点法作图可得 2×$\frac{π}{6}$+φ=$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∴函数f(x)=sin(2x+$\frac{π}{6}$).
∴将y=f(x)的图象向右平移$\frac{π}{6}$个单位后,得到的函数图象的解析式为y=sin[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=sin(2x-$\frac{π}{6}$).
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
2.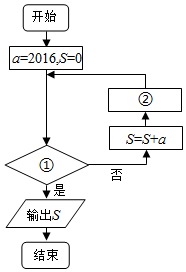 如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
 如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )| A. | ①a<0?,②a=a-3 | B. | ①a<0?,②a=a+3 | C. | ①a>0?,②a=a-3 | D. | ①a>0?,②a=a+3 |
19.执行如图所示的程序框图,则输出i的值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 55 |
16.已知直线l1:A1x+B1y+1=0,直线l2:A2x+B2y+1=0,A1,A2,B1,B2∈R,则“l1⊥l2”的充分且必要条件是( )
| A. | A1A2-B1B2=0 | B. | A1A2+B1B2=0 | C. | A1B2-A2B1=0 | D. | A1B2+A2B1=0 |
1.若直线l与直线y=2,x=4分别交于点P,Q,且线段PQ的中点坐标为(1,-1),则直线l的斜率为( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |