题目内容
(本小题满分12分)已知数列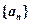 、
、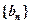 的前n项和分别为
的前n项和分别为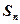 、
、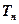 ,
,
且满足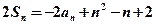 ,
,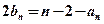 .
.
(Ⅰ)求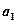 、
、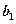 的值,并证明数列
的值,并证明数列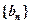 是等比数列;
是等比数列;
(Ⅱ)试确定实数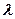 的值,使数列
的值,使数列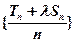 是等差数列.
是等差数列.
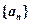 、
、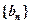 的前n项和分别为
的前n项和分别为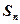 、
、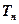 ,
,且满足
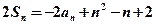 ,
,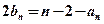 .
.(Ⅰ)求
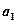 、
、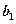 的值,并证明数列
的值,并证明数列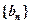 是等比数列;
是等比数列;(Ⅱ)试确定实数
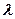 的值,使数列
的值,使数列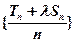 是等差数列.
是等差数列.略
(Ⅰ)由已知,得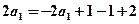 ∴
∴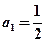 ∴
∴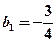
由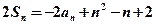 ,得
,得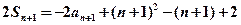
两式作差得: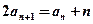 。
。
∴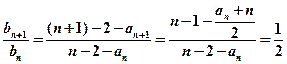 。
。
∴数列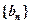 是以
是以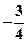 为首项,
为首项,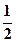 为公比的等比数列。
为公比的等比数列。
(Ⅱ)由(Ⅰ)知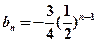 , ∴
, ∴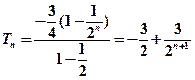
∵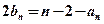 ∴
∴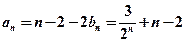
∴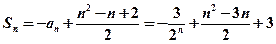
∵数列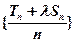 是等差数列的充要条件是
是等差数列的充要条件是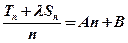 (A、B为常数)
(A、B为常数)
即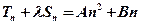
又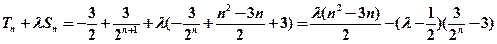
∴当且仅当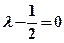 即
即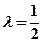 时数列
时数列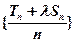 是等差数列。
是等差数列。
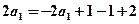 ∴
∴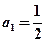 ∴
∴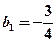
由
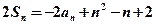 ,得
,得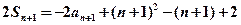
两式作差得:
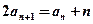 。
。∴
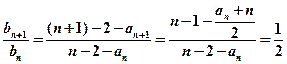 。
。∴数列
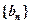 是以
是以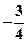 为首项,
为首项,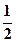 为公比的等比数列。
为公比的等比数列。(Ⅱ)由(Ⅰ)知
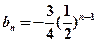 , ∴
, ∴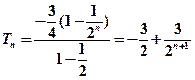
∵
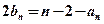 ∴
∴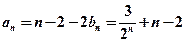
∴
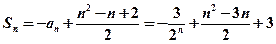
∵数列
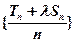 是等差数列的充要条件是
是等差数列的充要条件是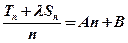 (A、B为常数)
(A、B为常数)即
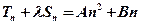
又
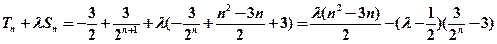
∴当且仅当
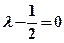 即
即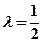 时数列
时数列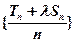 是等差数列。
是等差数列。
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
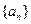 的前n项和为
的前n项和为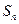 ,
,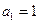 ,
,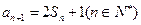 ,等差数列
,等差数列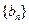 中
中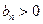
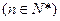 ,且
,且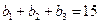 ,又
,又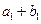 、
、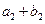 、
、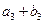 成等比数列.
成等比数列.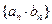 的前n项和
的前n项和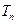 .
. 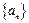 满足
满足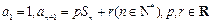 ,
,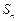 为数列
为数列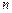 项和.
项和.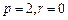 时,求
时,求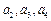 的值;
的值;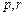 ,使得数列
,使得数列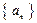 的前
的前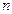 项和为
项和为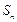 ,若对任意的
,若对任意的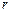 ,
,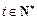 ,都有
,都有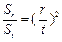 .
.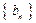 的第
的第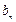 是数列
是数列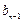 项
项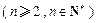 ,且
,且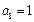 ,
,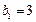 ,求数列
,求数列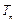 .
.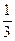 )是函数
)是函数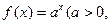 且
且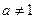 )的图象上一点,等比数列
)的图象上一点,等比数列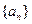 的前n项和为
的前n项和为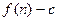 ,数列
,数列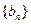
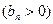 的首项为c,且前n项和
的首项为c,且前n项和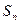 满足
满足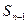 =
=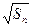 +
+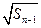 (n
(n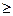 2).
2).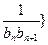 前n项和为
前n项和为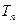 ,问
,问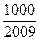 的最小正整数n是多少?
的最小正整数n是多少?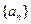 的前n项和为
的前n项和为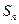 ,数列
,数列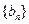 满足:
满足: 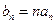 ,且数列
,且数列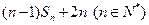 .
.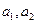 的值;
的值;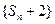 是等比数列;
是等比数列;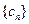 ,若
,若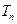 ,求证:
,求证: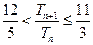 .
.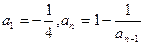
 ,求
,求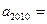
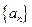 的前
的前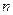 项和为
项和为 ,且
,且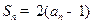 ,则
,则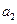 ( )
( ) 
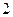
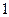
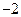
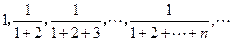 的前
的前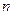 项和为( )
项和为( )