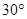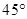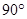题目内容
若α、β是两个不同的平面,m、n是两条不同直线,则下列命题不正确的是
| A.α∥β,m⊥α,则m⊥β |
| B.m∥n,m⊥α,则n⊥α |
| C. n∥α,n⊥β,则α⊥β |
D.α β=m,n与α、β所成的角相等,则m⊥n β=m,n与α、β所成的角相等,则m⊥n |
D
解析试题分析:对于选项A,由于α∥β,m⊥α,如果一条直线垂直于平行平面中的一个,必定垂直与另一个平面,那恶么显然成立。
对于选项B,两条平行线中一条垂直该平面,则另一条也垂直于该平面,成立。
对于选项C,一条直线平行与一个平面,还垂直于另一个平面,在这两个平面必行垂直也成立。
对于选项D,由于与两个相交平面所成的角相等的直线,不一定与其交线垂直,因此错误,故选D.
考点:本试题考查了空间中点线面的位置挂系运用
点评:解决该试题的关键是对于空间中的线面垂直和面面垂直关系的判定定理和性质定理的熟练运用。同时能借助于现实中的长方体特殊模型来加以判定,属于基础题。

练习册系列答案
相关题目
如图所示,正方体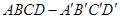 的棱长为1,O是平面
的棱长为1,O是平面 的中心,则O到平面
的中心,则O到平面 的距离是( )
的距离是( )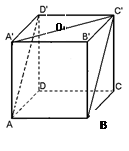
A. | B.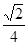 | C.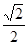 | D.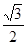 |
已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是 ( )
| A.若α⊥γ,α⊥β,则γ∥β | B.若m∥n,m?α,n?β,则α∥β |
| C.若m∥n,m∥α,则n∥α | D.若m∥n,m⊥α,n⊥β,则α∥β |
椭圆 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得 点在平面
点在平面

 上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
| A.75° | B.60° | C.45° | D.30° |
若a、b表示两条不同直线,α、β表示两个不同平面,则下列命题正确的是( )
A.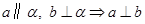 | B.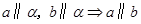 |
C.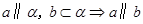 | D. |
已知两条直线 ,
, ,两个平面
,两个平面 ,
,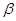 ,给出下面四个命题:
,给出下面四个命题:
①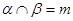 ,
,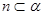
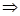
 ∥
∥ 或者
或者 ,
, 相交
相交
② ∥
∥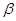 ,
, ,
,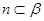
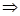
 ∥
∥
③ ∥
∥ ,
, ∥
∥
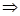
 ∥
∥
④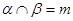 ,
,  ∥
∥
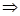
 ∥
∥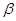 或者
或者 ∥
∥
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
已知正三棱柱ABC—A1B1C1中,A1B⊥CB1,则A1B与AC1所成的角为( )
| A.450 | B.600 | C.900 | D.1200 |
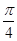 和
和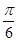 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )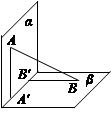
 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 底面
底面 ,点
,点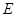 是侧面
是侧面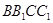 的中心,若
的中心,若 ,则直线
,则直线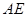 与平面
与平面