题目内容
15.直线x=t(t>0),与函数f(x)=x2+1,g(x)=lnx的图象分别交于A,B两点,则|AB|最小值( )| A. | $\frac{1}{2}+ln2$ | B. | $\frac{1}{2}+2ln2$ | C. | $\frac{3}{2}+2ln2$ | D. | $\frac{3}{2}+\frac{1}{2}ln2$ |
分析 将两个函数作差,得到函数y=f(x)-g(x),再求此函数的最小值即可得到|AB|最小值.
解答 解:设函数y=f(x)-g(x)=x2-lnx+1,求导数得
y′=2x-$\frac{1}{x}$=$\frac{2{x}^{2}-1}{x}$,
当0<x<$\frac{\sqrt{2}}{2}$时,y′<0,函数在(0,$\frac{\sqrt{2}}{2}$)上为单调减函数,
当x>时,y′>0,函数在($\frac{\sqrt{2}}{2}$,+∞)上为单调增函数,
所以当x=$\frac{\sqrt{2}}{2}$时,所设函数的最小值为$\frac{3}{2}$+$\frac{1}{2}$ln2,
所以|AB|最小值为$\frac{3}{2}$+$\frac{1}{2}$ln2,
故选:D.
点评 本题主要考查函数最值的求法,利用导数研究函数的极值是解决本题的关键.

练习册系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 垂直于同一直线的两条直线互相平行 | |
| B. | 垂直于同一平面的两条直线互相平行 | |
| C. | 垂直于同一平面的两个平面互相平行 | |
| D. | 平行于同一平面的两条直线互相平行 |
10. 一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
 一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
20.曲线$y=\frac{-2}{x+2}+1在点(-1,-1)$处的切线方程为( )
| A. | y=2x+1 | B. | y=2x-1 | C. | y=-2x-3 | D. | y=-2x-2 |
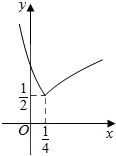 如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).
如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).