题目内容
2.已知函数f(x)=log2(ax2-3x+2)(1)若f(1)<2,求a的取值范围;
(2)若a=1,求满足$(\frac{1}{2})^{t}$<f(3)的t的取值范围.
分析 (1)化简可得f(1)=log2(a-1)<2,从而解得;
(2)当a=1时,f(3)=log2(9-3×3+2)=1,从而可得$(\frac{1}{2})^{t}$<f(3)=1,从而解得.
解答 解:(1)∵f(1)=log2(a-1)<2,
∴0<a-1<4,
∴1<a<5;
(2)当a=1时,f(3)=log2(9-3×3+2)=1,
∴$(\frac{1}{2})^{t}$<f(3)=1,
∴t>0.
点评 本题考查了对数函数的性质应用及复合函数的性质应用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
10.两个圆锥的母线长相等,侧面展形圆心角分别为120°和240°,体积分别为V1和V2,则V1:V2等于( )
| A. | 1:8 | B. | 1:10 | C. | $\sqrt{10}$:10 | D. | $\sqrt{5}$:5 |
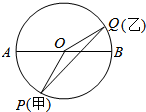 如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.
如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式. 如图:点E、F、G、H分别是空间四边形的边AB、BC、CD、DA上的点,且直线EH与直线FG交于点O,求证:B、D、O三点共线.
如图:点E、F、G、H分别是空间四边形的边AB、BC、CD、DA上的点,且直线EH与直线FG交于点O,求证:B、D、O三点共线.