题目内容
已知函数 (ω>0,
(ω>0, .其图象的最高点与相邻对称中心的距离为
.其图象的最高点与相邻对称中心的距离为 ,且过点
,且过点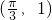 .
.
(Ⅰ)求函数f(x)的达式;
(Ⅱ)在△ABC中.a、b、c分别是角A、B、C的对边,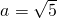 ,
, ,角C为锐角.且满足2a=4asinC-csinA,求c的值.
,角C为锐角.且满足2a=4asinC-csinA,求c的值.
解:(Ⅰ)由于 .(2分)
.(2分)
∵最高点与相邻对称中心的距离为 ,则
,则 ,即T=π,(3分)
,即T=π,(3分)
∴ ,∵ω>0,∴ω=2.(4分)
,∵ω>0,∴ω=2.(4分)
又f(x)过点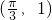 ,∴
,∴ ,即
,即 ,∴
,∴ .(5分)
.(5分)
∵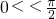 ,∴
,∴ ,
,
∴ .(6分)
.(6分)
(Ⅱ)2a=4asinC-csinA,由正弦定理可得 2sinA=4sinAsinC-sinCsinA,解得 .(8分)
.(8分)
又∵ ,∴
,∴ .(9分)
.(9分)
又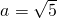 ,
, ,∴b=6,(11分)
,∴b=6,(11分)
由余弦定理得c2=a2+b2-2abcosC=21,∴ .(12分)
.(12分)
分析:(Ⅰ)利用两角和差的正弦公式化简函数的解析式,根据函数的周期求ω,把所给的点的坐标代入求出Φ的值,从而确定出函数的解析式.
(Ⅱ)根据条件2a=4asinC-csinA,由正弦定理求得sinC的值,可得cosC的值,再由余弦定理求得c的值.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,两角和差的正弦公式、正弦定理和余弦定理的应用,两个向量的数量积的定义,属于中档题.
 .(2分)
.(2分)∵最高点与相邻对称中心的距离为
 ,则
,则 ,即T=π,(3分)
,即T=π,(3分)∴
 ,∵ω>0,∴ω=2.(4分)
,∵ω>0,∴ω=2.(4分)又f(x)过点
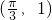 ,∴
,∴ ,即
,即 ,∴
,∴ .(5分)
.(5分)∵
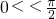 ,∴
,∴ ,
,∴
 .(6分)
.(6分)(Ⅱ)2a=4asinC-csinA,由正弦定理可得 2sinA=4sinAsinC-sinCsinA,解得
 .(8分)
.(8分)又∵
 ,∴
,∴ .(9分)
.(9分)又
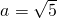 ,
, ,∴b=6,(11分)
,∴b=6,(11分)由余弦定理得c2=a2+b2-2abcosC=21,∴
 .(12分)
.(12分)分析:(Ⅰ)利用两角和差的正弦公式化简函数的解析式,根据函数的周期求ω,把所给的点的坐标代入求出Φ的值,从而确定出函数的解析式.
(Ⅱ)根据条件2a=4asinC-csinA,由正弦定理求得sinC的值,可得cosC的值,再由余弦定理求得c的值.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,两角和差的正弦公式、正弦定理和余弦定理的应用,两个向量的数量积的定义,属于中档题.

练习册系列答案
相关题目
已知函数,f(x)=
,则复合函数f{f[f(-1)]}=( )
|
| A、x2+1 |
| B、π2+1 |
| C、-π |
| D、0 |