题目内容
17．若${（2-3x）}^{\frac{3}{4}}$+${（x-1）}^{\frac{2}{3}}$有意义，则x=（-∞，$\frac{2}{3}$]．分析 化分数指数幂与根式，由偶次根下内部的代数式大于等于0求得x的范围．
解答 解：${（2-3x）}^{\frac{3}{4}}$+${（x-1）}^{\frac{2}{3}}$=$\root{4}{（2-3x）^{3}}+\root{3}{（x-1）^{2}}$，
要使原式有意义，则2-3x≥0，解得：x$≤\frac{2}{3}$．
∴x∈（-∞，$\frac{2}{3}$]．
故答案为：（-∞，$\frac{2}{3}$]．
点评 本题考查函数的定义域及其求法，考查分数指数幂与根式的互化，是基础题．
练习册系列答案
相关题目
7．设数列（an}的前n项和为Sn，如果an=$\frac{1}{（2n-1）（2n+1）}$，那么S5等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{5}{11}$ | C． | $\frac{4}{9}$ | D． | $\frac{5}{9}$ |
5．已知|lga|=|lgb|（a＞0，b＞0），则（ ）
| A． | a=b | B． | a=b或ab=1 | C． | a=±b | D． | ab=1 |
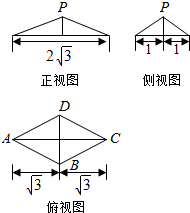已知四棱锥P-ABCD的三视图如图所示，其中俯视图是菱形，正视图和侧视图都是等腰三角形，已知M为BC上一点，且BM=$\frac{1}{2}$，PA⊥PM．