题目内容

已知正数a、b、c满足a+b+c=1，求证：（1-a）
a
≤
2
3
9
．
考点：不等式的证明
专题：证明题
分析：依题意知，0＜a＜1，令y=（1-a）
a
，可求得y2=（1-a）2a=
1
2
×2a（1-a）（1-a），利用基本不等式2a（1-a）（1-a）≤[
2a+(1-a)+(1-a)
3
]3=
4
27
，再开方即可证得结论．
解答： 解：∵a+b+c=1，a，b，c为正数，∴0＜a＜1，
令y=（1-a）
a
，
则y2=（1-a）2a=
1
2
×2a（1-a）（1-a）
≤
1
2
×[
2a+(1-a)+(1-a)
3
]3=
4
27
，
∴y≤
2
3
9
，即（1-a）
a
≤
2
3
9
．
点评：本题考查不等式的证明，考查构造函数思想，利用基本不等式2a（1-a）（1-a）≤[
2a+(1-a)+(1-a)
3
]3=
4
27
是关键，属于中档题．
练习册系列答案
相关题目
复数z的虚部为1，且
z
1+i
为纯虚数，其中i是虚数单位，则z=（　　）
A、-1-iB、1+i
C、1-iD、-1+i
已知f（x）=ax3+bx2+c的图象经过点（0，1），且在x=1处的切线方程是y=-2x+1
（1）求y=f（x）的解析式；
（2）求y=f（x）的单调递增区间．
设数列{an}满足
an+1
an
=q，且q≠0，数列{bn}满足bn=na1+（n-1）a2+（n-2）a3+…+2an-1+an（n∈N*），已知b1=m，b2=
3m
2
，其中m≠0：
（Ⅰ）当m=1时，求bn；
（Ⅱ）设Sn为数列{an}的前n项和，若对于任意的正整数n，都有Sn2-4sn+3≤0恒成立，求实数m的取值范围．
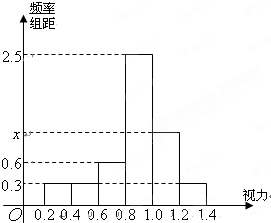为了解某校高三学生的视力情况，随机抽查了该校50名高三学生，得到如图所示的频率分布直方图．
（Ⅰ）求图中x的值；
（Ⅱ）若从视力在[0.2，0.6）的学生中随机选取2人，求这2人视力均在[0.2，0.4）的概率．
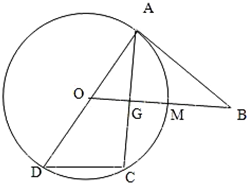如图所示，已知AD为圆O的直径，直线BA与圆O相切于点A，直线OB与弦AC垂直并相交于点G，与弧AC相交于M，连接DC，AB=10，AC=12，则BM=
 
．
对于以下结论：
①若y=f（x）是奇函数，则f（0）=0；
②已知p：事件A、B是对立事件，q：事件A、B是互斥事件，则p是q的必要但不充分条件；
③
ln5
5
＜
ln3
3
＜
1
e
（e为自然对数的底数）；
④若
a
=（1，2），
b
=（0，-1），则
b
在
a
上的投影为
2
5
5
；
⑤若随机变量ξ～N（1，4），则P（ξ≤1）=
1
2
．
其中，正确结论的序号为
 
．
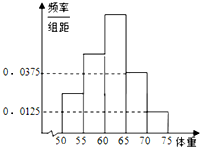为了了解高三学生的身体状况，抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图）．已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为15，则抽取的男生总人数是
 
．
化简：
cos15°-2sin15°
sin15°
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网