题目内容
(文做)设
=(sinx,
),
=(
,-
cosx),且
∥
,x∈(
,π),则x=( )
| a |
| 5 |
| 4 |
| b |
| 1 |
| 5 |
| 1 |
| 2 |
| a |
| b |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:三角函数的化简求值,平面向量共线(平行)的坐标表示
专题:三角函数的求值
分析:通过向量平行的充要条件,化简方程求解即可.
解答:
解:设
=(sinx,
),
=(
,-
cosx),且
∥
,
可得
×
=-
sinxcosx,
所以sin2x=-1,x∈(
,π),
所以2x=
,x=
.
故选:D.
| a |
| 5 |
| 4 |
| b |
| 1 |
| 5 |
| 1 |
| 2 |
| a |
| b |
可得
| 5 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
所以sin2x=-1,x∈(
| π |
| 2 |
所以2x=
| 3π |
| 2 |
| 3π |
| 4 |
故选:D.
点评:本题考查向量的共线,三角函数的化简求值,基本知识的考查.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
函数f(x)=ax-2+loga(x-1)(a>0且a≠1),在x∈[2,3]上的最大值与最小值之和为a,则a等于( )
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
三个数a=0.22,b=log202,c=20.1之间的大小关系是( )
| A、a<c<b |
| B、a<b<c |
| C、b<a<c |
| D、b<c<a |
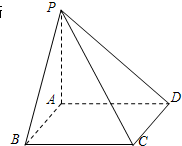 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
 已知定义在R上的奇函数f(x),当x∈(0,+∞)时的解析式为y=x2+2.
已知定义在R上的奇函数f(x),当x∈(0,+∞)时的解析式为y=x2+2.