题目内容
16.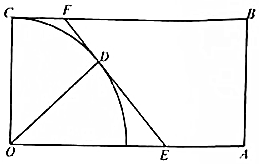 如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.
如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.(1)试求观光道路EF长度的最大值;
(2)公园计划在道路EF右侧种植草坪,试求草坪ABFE面积S的最大值.
分析 (1)求出∠DOF=$\frac{π}{4}$-$\frac{θ}{2}$,分别求出DE,DF,从而求出EF的表达式,求出EF的最大值即可;
(2)求出S=S矩形OABC-S梯形OEFC的表达式,求出函数的导数,根据函数的单调性求出S的最大值即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.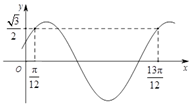 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,$φ=\frac{π}{6}$ | B. | $ω=\frac{1}{2}$,$φ=\frac{π}{6}$ | C. | ω=2,$φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2}$,$φ=\frac{π}{3}$ |
1.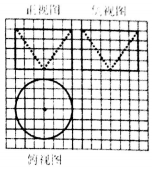 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )
 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )| A. | 39π | B. | 48π | C. | 57π | D. | 63π |
5.命题p:若x>y,则tanx>tany;命题q:x2+y2≥2xy.下列命题为假命题的是( )
| A. | p∨q | B. | p∧q | C. | ¬p | D. | q |
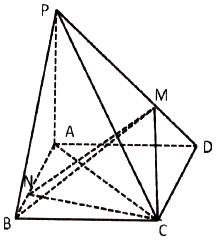 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$. 已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.
已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.