题目内容
5.命题p:若x>y,则tanx>tany;命题q:x2+y2≥2xy.下列命题为假命题的是( )| A. | p∨q | B. | p∧q | C. | ¬p | D. | q |
分析 先判断命题p,q的真假,进而根据复合命题真假判断的真值表,可得答案.
解答 解:若x为钝角,y为锐角,则x>y,tanx<tany,
故命题p:若x>y,则tanx>tany,为假命题;
(x-y)2≥0恒成立,故命题q:x2+y2≥2xy为真命题;
故命题p∨q,¬p均为真命题,
p∧q为假命题,
故选:B
点评 本题以命题的真假判断与应用为载体,考查了复合命题,正切函数,不等式的证明等知识点,难度基础.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.若关于x的不等式xex-ax+a<0的解集为(m,n)(n<0),且(m,n)中只有一个整数,则实数a的取值范围是( )
| A. | $(\frac{2}{{3{e^2}}},\frac{1}{e})$ | B. | $[\frac{2}{{3{e^2}}},\frac{1}{e})$ | C. | $(\frac{2}{{3{e^2}}},\frac{1}{2e})$ | D. | $[\frac{2}{{3{e^2}}},\frac{1}{2e})$ |
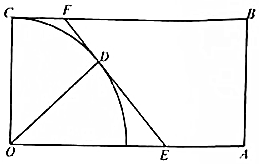 如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.
如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.