题目内容
4.若复数z满足|z|=1(i为虚数单位),则|z-2i|的最小值是1.分析 复数z满足|z|=1(i为虚数单位),设z=cosθ+isinθ,θ∈[0,2π).利用复数模的计算公式与三角函数求值即可得出.
解答 解:∵复数z满足|z|=1(i为虚数单位),
设z=cosθ+isinθ,θ∈[0,2π).
则|z-2i|=|cosθ+i(sinθ-2)|=$\sqrt{co{s}^{2}θ+(sinθ-2)^{2}}$=$\sqrt{5-4sinθ}$≥1,当且仅当sinθ=1时取等号.
故答案为:1.
点评 本题考查了复数的运算法则、模的计算公式及其三角函数求值,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
14.抛物线y=9x2的焦点坐标为( )
| A. | ($\frac{1}{36}$,0) | B. | (0,$\frac{1}{36}$) | C. | ($\frac{9}{4}$,0) | D. | (0,$\frac{9}{4}$) |
13.已知θ∈(π,2π),$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(cosθ,sinθ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则cosθ的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | ±$\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
18.直线2x-y-4=0与抛物线y2=6x交于A、B两点,则线段AB的长度为( )
| A. | $\frac{{\sqrt{265}}}{2}$ | B. | $\frac{{\sqrt{285}}}{2}$ | C. | $\frac{{\sqrt{305}}}{2}$ | D. | $\frac{{\sqrt{335}}}{2}$ |
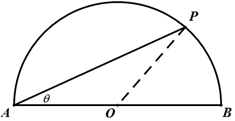 运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.
运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.