题目内容
若直线
经过圆
的圆心，则
的值为
A． | B． | C． | D． |
B
解析试题分析：因为题目中直线经过圆的圆心，则说明圆心坐标满足直线方程，圆心为（1，-2），因此可知1-2+a=0,故可知a=1.选B.
考点：直线与圆
点评：直线与圆的位置关系是常规试题，难度不大，只要细心即可得分。
练习册系列答案
相关题目
圆：x²+y²-4x+6y=0和圆：x²+y²-6x=0交于A,B两点，则AB的垂直平分线的方程是 ( )
| A．x+y+3=0 | B．2x-y-5="0" | C．3x-y-9=0 | D．4x-3y+7=0 |
已知圆C：
和点
,P是圆上一点，线段BP的垂直平分线交CP于M点，则M点的轨迹方程是（ ）。
A． . | B． |
C． | D． |
圆
的周长是（ ）
A． | B． | C． | D． |
已知圆
和直线
相交于P,Q两点，则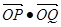
的值为（O为坐标原点）（ ）
| A．12 | B．16 | C．21 | D．25 |
若点P（3，－1）为圆
的弦AB的中点，则直线AB的方程为（ ）
| A．x+y-2=0 | B．2x－y-7=0 | C．2x+y-5=0 | D．x－y-4=0 |
已知集合
,
。若存在实数
使得
成立,称点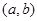
为“￡”点，则“￡”点在平面区域
内的个数是
| A．0 | B．1 | C．2 | D．无数个 |
圆
关于原点
对称的圆的方程为 ( )
A． | B． |
C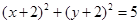． | D． |
点
在圆
内，则直线
和已知圆的公共点个数为
| A．0 | B．1 | C．2 | D．不能确定 |