题目内容
已知圆 和直线
和直线 相交于P,Q两点,则
相交于P,Q两点,则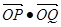 的值为(O为坐标原点)( )
的值为(O为坐标原点)( )
| A.12 | B.16 | C.21 | D.25 |
C
解析试题分析:根据题意,由于圆 和直线
和直线 相交于P,Q两点,则联立方程组,可知
相交于P,Q两点,则联立方程组,可知
设两点的坐标为 ,则由韦达定理可知
,则由韦达定理可知 ,
, 而对于
而对于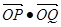 则等于
则等于 ,将上式代入化简可知结果为21.故选C.
,将上式代入化简可知结果为21.故选C.
考点:向量的数量积运算
点评:直线与圆的位置关系的运用,主要是勾股定理的运用。属于基础题。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知集合 ,集合
,集合 ,若
,若 ,则实数
,则实数 可以取的一个值是( )
可以取的一个值是( )
A. | B. | C. | D. |
若函数 的图象在x=0处的切线
的图象在x=0处的切线 与圆
与圆 相离,则
相离,则 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.在圆外 | B.在圆内 | C.在圆上 | D.不能确定 |
已知圆 与直线
与直线 都相切,圆心在直线
都相切,圆心在直线 上,则圆
上,则圆 的方( )
的方( )
A. | B. |
C. | D. |
圆 与圆
与圆 的位置关系为( )
的位置关系为( )
| A.内切 | B.相交 | C.外切 | D.相离 |
若直线
 经过圆
经过圆
 的圆心,则
的圆心,则 的值为
的值为
A. | B. | C. | D. |
圆C1:  与圆C2:
与圆C2: 的位置关系是( )
的位置关系是( )
| A.外离 | B.外切 | C.内切 | D.相交 |
方程x2+y2+2x-4y-6=0表示的图形是( )
A.以(1,-2)为圆心, 为半径的圆; 为半径的圆; | B.以(1,2)为圆心, 为半径的圆; 为半径的圆; |
C.以(-1,-2)为圆心, 为半径的圆; 为半径的圆; | D.以(-1,2)为圆心, 为半径的圆 为半径的圆 |
 :
: 与圆
与圆 :
: 位置关系是( )
位置关系是( )