题目内容
已知集合 ,
,


 。若存在实数
。若存在实数 使得
使得 成立,称点
成立,称点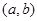 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是
内的个数是
| A.0 | B.1 | C.2 | D.无数个 |
A
解析试题分析:由A∩B≠∅得,na+b=3n2+12,(A∩B=∅时x=n=m),
对于任意的整数n,动点(a,b)的集合是直线l:na+b=3n2+12,
由于圆x2+y2=108的圆心到直线l的距离d=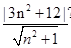 =3(
=3( )≥6
)≥6 .
.
∵n为整数,∴上式不能取等号,所以直线和圆相离.
所以两者无有公共点.
故选A.
考点:本题主要考查集合的运算,直线与圆的位置关系,均值定理的应用。
点评:中档题,本题综合性较强,首先根据两集合交集不空,得到方程na+b=3n2+12有实数解。利用数形结合思想,将问题转化成圆心到直线的距离。

练习册系列答案
相关题目
直线 R
R 与圆
与圆 的交点个数是( )
的交点个数是( )
| A.0 | B.1 | C.2 | D.无数个 |
已知圆 与直线
与直线 都相切,圆心在直线
都相切,圆心在直线 上,则圆
上,则圆 的方( )
的方( )
A. | B. |
C. | D. |
若直线
 经过圆
经过圆
 的圆心,则
的圆心,则 的值为
的值为
A. | B. | C. | D. |
圆C1:  与圆C2:
与圆C2: 的位置关系是( )
的位置关系是( )
| A.外离 | B.外切 | C.内切 | D.相交 |
已知圆的方程为 ,若抛物线过点
,若抛物线过点 ,
, 且以圆的切线为准线,则抛物线的焦点的轨迹方程是
且以圆的切线为准线,则抛物线的焦点的轨迹方程是
A. | B. |
C. | D. |
已知直线l:3x+4y-12=0与圆C: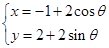 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( )
| A.相切 | B.相离 | C.相交但直线不过圆心 | D.直线过圆心 |
 :
: 与圆
与圆 :
: 位置关系是( )
位置关系是( ) 和圆
和圆 在同一坐标系的图形只能是( )
在同一坐标系的图形只能是( )