题目内容
圆:x²+y²-4x+6y=0和圆:x²+y²-6x=0交于A,B两点,则AB的垂直平分线的方程是 ( )
| A.x+y+3=0 | B.2x-y-5="0" | C.3x-y-9=0 | D.4x-3y+7=0 |
C
解析试题分析:解:圆:x2+y2-4x+6y="0" 的圆心坐标为(2,-3),圆:x2+y2-6x=0的圆心坐标为(3,0),由题意可得AB的垂直平分线的方程就是两圆的圆心所在的直线的方程,由两点式求得AB的垂直平分线的方程是  ,即3x-y-9=0,故答案为C
,即3x-y-9=0,故答案为C
考点:直线方程
点评:本题主要考查用两点式求直线方程的方法,判断AB的垂直平分线的方程就是两圆的圆心所在的直线的方程,是解题的关键,属于基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
与直线 和圆
和圆 都相切的半径最小的圆的方程是( )
都相切的半径最小的圆的方程是( )
A. | B. |
C. | D. |
直线 截圆
截圆 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A. | B. | C. | D. |
已知集合 ,集合
,集合 ,若
,若 ,则实数
,则实数 可以取的一个值是( )
可以取的一个值是( )
A. | B. | C. | D. |
若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2 ,则实数a的值为
,则实数a的值为
A.-1或 | B.1或3 | C.-2或6 | D.0或4 |
直线 R
R 与圆
与圆 的交点个数是( )
的交点个数是( )
| A.0 | B.1 | C.2 | D.无数个 |
若方程 表示圆,则
表示圆,则 的取值范围是( )
的取值范围是( )
A.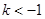 | B. | C. | D. |
若直线
 经过圆
经过圆
 的圆心,则
的圆心,则 的值为
的值为
A. | B. | C. | D. |



