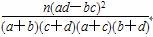题目内容
某省高中学校自实施素质教育以来,学生社团得到迅猛发展,某校高一新生中的五名同学打算参加“春晖文学社”、“舞者轮滑俱乐部”、“篮球之家”、“围棋苑”四个社团.若每个社团至少有一名同学参加,每名同学至少参加一个社团且只能参加一个社团.且其中甲不参加“围棋苑”,则不同的参加方法的种数为( )
A.72 B.108
C.180 D.216
C
[解析] 设五名同学分别为甲、乙、丙、丁、戊,由题意,如果甲不参加“围棋苑”,有下列两种情况:
(1)从乙、丙、丁、戊中选一人(如乙)参加“围棋苑”,有C 种方法,然后从甲与丙、丁、戊共4人中选2人(如丙、丁)并成一组与甲、戊分配到其他三个社团中,有C
种方法,然后从甲与丙、丁、戊共4人中选2人(如丙、丁)并成一组与甲、戊分配到其他三个社团中,有C A
A 种方法,故共有C
种方法,故共有C C
C A
A 种参加方法;
种参加方法;
(2)从乙、丙、丁、戊中选2人(如乙、丙)参加“围棋苑”,有C 种方法,甲与丁、戊分配到其他三个社团中有A
种方法,甲与丁、戊分配到其他三个社团中有A 种方法,这时共有C
种方法,这时共有C A
A 种参加方法;
种参加方法;
综合(1)(2),共有C C
C A
A +C
+C A
A =180种参加方法.
=180种参加方法.
[解法探究] 由于甲是特殊元素,故按甲进行分类.
第一类,甲自己去一个社团,有C 种选法,将其余4人中选2人有C
种选法,将其余4人中选2人有C 种选法,将这2人和其余2人分派到三个社团共有A
种选法,将这2人和其余2人分派到三个社团共有A 种方法,∴共有C
种方法,∴共有C C
C A
A =108种.
=108种.
第二类,甲与另外一人同去一个社团,先安排甲有C 种选法,然后将剩余4人分派到四个社团有A
种选法,然后将剩余4人分派到四个社团有A 种,∴共有C
种,∴共有C A
A =72种,∴总共有108+72=180种参加方法.
=72种,∴总共有108+72=180种参加方法.

某中学研究性学习小组,为了考查高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了50名学生.调查结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(1)试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
|
| 爱看课外书 | 不爱看课外书 | 总计 |
| 作文水平好 | |||
| 作文水平一般 | |||
| 总计 |
(2)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附表:
| P(K2≥k)或P(χ2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2(或χ2)=