题目内容
5.设函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)其图象上最高点M的坐标是(2,$\sqrt{2}$),曲线上点P由点M运动到相邻的最低点N时,在点Q(6,0)处越过x轴.(1)求A,ω,φ的值;
(2)函数f(x)的图象能否通过平移变换得到一个奇函数的图象?若能,写出变换方法;若不能,说明理由.
分析 (1)根据函数的最高点的坐标以及函数对称中心,建立方程关系即可求A,ω,φ的值;
(2)利用函数平移关系以及函数奇偶性的性质进行判断即可.
解答 解:(1)∵图象上最高点M的坐标是(2,$\sqrt{2}$),
∴A=$\sqrt{2}$,
∵曲线上点P由点M运动到相邻的最低点N时,在点Q(6,0)处越过x轴,
∴Q(6,0)是一个对称中心,
则$\frac{T}{4}$=6-2=4,即函数的周期T=4×4=16,
∵T=$\frac{2π}{ω}$=16,
∴ω=$\frac{π}{8}$.
即函数y=$\sqrt{2}$sin($\frac{π}{8}$x+φ),
∵当x=2时,y=$\sqrt{2}$,
∴$\sqrt{2}$sin($\frac{π}{8}$×2+φ)=$\sqrt{2}$,
即sin($\frac{π}{4}$+φ)=1,
即$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,即φ=kπ+$\frac{π}{4}$,
∵|φ|<π,
∴当k=0时,φ=$\frac{π}{4}$,
即函数求A=$\sqrt{2}$,ω=$\frac{π}{8}$,φ=$\frac{π}{4}$;
(2)∵A=$\sqrt{2}$,ω=$\frac{π}{8}$,φ=$\frac{π}{4}$;
∴函数y=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$)=$\sqrt{2}$sin[$\frac{π}{8}$(x+2)],
将函数向右平移2个单位得到y=$\sqrt{2}$sin[$\frac{π}{8}$(x-2+2)]=$\sqrt{2}$sin$\frac{π}{8}$x为奇函数,满足条件,
即函数f(x)的图象可以通过平移变换得到一个奇函数的图象.
点评 本题主要考查三角函数解析式的确定以及三角函数性质的考查,根据条件确定A,ω和φ的值是解决本题的关键.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | 6 | B. | 3 | C. | 2 | D. | 1 |
| A. | 2016 | B. | $\frac{4033}{2}$ | C. | 2017 | D. | $\frac{4035}{2}$ |
| A. | [-3,3] | B. | (-3,3) | C. | (-∞,3] | D. | [3,+∞) |
 在校园文化艺术节的比赛中,七位评委老师为某参赛选手打分,打出的分数如“茎叶图”所示,若去掉一个最高分和一个最低分后,则所剩数据的方差为$\frac{8}{5}$.
在校园文化艺术节的比赛中,七位评委老师为某参赛选手打分,打出的分数如“茎叶图”所示,若去掉一个最高分和一个最低分后,则所剩数据的方差为$\frac{8}{5}$.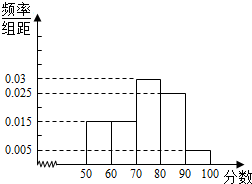 为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题: