题目内容
18.判断函数y=sin($\frac{5π}{2}$-x)的奇偶性.分析 将函数解析式化简可得y=cosx,从而判断出函数的奇偶性.
解答 解:函数的定义域为R,
y=sin($\frac{5π}{2}$-x)=sin($\frac{π}{2}$-x)=cosx.
∴函数y=sin($\frac{5π}{2}$-x)是偶函数.
点评 本题考查了三角函数的恒等变换,余弦函数的奇偶性,属于基础题.

练习册系列答案
相关题目
6.已知实数x、y满足$\left\{\begin{array}{l}{4x+y-9≥0}\\{x-y-1≤0}\\{y≤3}\end{array}\right.$,若x-ky的最大值是-1,则正数k的值为( )
| A. | 3 | B. | $\frac{5}{3}$ | C. | 3或$\frac{5}{3}$ | D. | 3或$\frac{5}{6}$ |
13.下列函数中,当自变量x变得很大时,随x的增大速度增大得最快的是( )
| A. | y=$\frac{1}{100}$ex | B. | y=100lnx | C. | y=x100 | D. | y=100•2x |
3.设定义在(0,+∞)上的单调函数f(x)对任意的x∈(0,+∞)都有f(f(x)-log2x)=6,则不等式f(a2+a)>5的解集为( )
| A. | {a|a>1} | B. | {a|a<-2或a>1} | C. | {a|-2<a<1} | D. | {a|a<-2} |
5.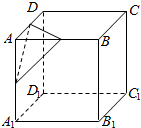 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )| A. | 此多面体的表面积为$\frac{47}{8}$a2 | B. | 体对角线AC1垂直于截面 | ||
| C. | 截面平行于平面CB1D1 | D. | 有10个顶点 |