题目内容
3.若正实数x,y满足x2+2xy-1=0,则2x+y的最小值为$\sqrt{3}$ .分析 由条件可得y=$\frac{1}{2x}$-$\frac{x}{2}$,代入2x+y=$\frac{1}{2}$(3x+$\frac{1}{x}$),利用基本不等式求出最值
解答 解:∵正实数x,y满足x2+2xy-1=0,
∴y=$\frac{1}{2x}$-$\frac{x}{2}$,
∴2x+y=2x+$\frac{1}{2x}$-$\frac{x}{2}$=$\frac{3}{2}$x+$\frac{1}{2x}$=$\frac{1}{2}$(3x+$\frac{1}{x}$)≥$\frac{1}{2}$×2$\sqrt{3x•\frac{1}{x}}$=$\sqrt{3}$,当且仅当x=$\frac{\sqrt{3}}{3}$时取等号,
∴2x+y的最小值为$\frac{\sqrt{3}}{3}$,
故答案为:$\sqrt{3}$
点评 本题考查了基本不等式的应用问题,解题的关键是2x+y=$\frac{3}{2}$x+$\frac{1}{2x}$,使它能利用基本不等式,是基础题目.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
13.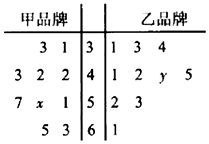 某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,为调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.
某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,为调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.
(1)求出x,y的值;
(2)以10天的销量为样本,估计100天的销量,请完成这两种品牌100天销量的2×2列联表,并判断是否有99%的把握认为品牌与“畅销日”天数相关.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d为样本容量)
 某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,为调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.
某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,为调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.(1)求出x,y的值;
(2)以10天的销量为样本,估计100天的销量,请完成这两种品牌100天销量的2×2列联表,并判断是否有99%的把握认为品牌与“畅销日”天数相关.
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲 | 50 | 50 | 100 |
| 乙 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
14.已知a=2,$b={125^{\frac{1}{6}}}$,c=log47,则下列不等式关系成立的是( )
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
11.已知变量x,y满足$\left\{\begin{array}{l}2x-y≤0\\ x-2y+3≥0\\ x≥0\end{array}\right.$,则z=8x•2y的最大值为( )
| A. | 33 | B. | 32 | C. | 35 | D. | 34 |
8.已知a∈R,则“a<3”是“|x+2|+|x-1|>a恒成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.与复数z的实部相等,虚部互为相反数的复数叫做z的共轭复数,并记作$\overline z$,若z=i(3-2i)(其中i为复数单位),则$\overline z$=( )
| A. | 3-2i | B. | 3+2i | C. | 2+3i | D. | 2-3i |
13.某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长,开展评选“校园之星”活动.规定各班每10人推选一名候选人,当各班人数除以10的余数大于7时再增选一名候选人,那么,各班可推选候选人人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )
| A. | y=[$\frac{x}{10}$] | B. | y=[$\frac{x+2}{10}$] | C. | y=[$\frac{x+3}{10}$] | D. | y=[$\frac{x+4}{10}$] |