题目内容
13.设△ABC中,角A,B,C的对边分别为a,b,c,给出如下四个命题:(1)若a,b,c成等差数列,则B≤$\frac{π}{3}$;
(2)若B>$\frac{π}{2}$,则logsinBsinA<logsinBcosC
(3)若b2=ac,则a2+c2-b2≥ac
(4)若sinA-sinB≤0,则A≤B
其中真命题的序号是(1)(3)(4)(要求填上所有真命题的序号)
分析 (1)由a,b,c成等差数列,根据等差数列的性质得到2b=a+c,解出b,然后利用余弦定理表示出cosB,把b的式子代入后,合并化简,利用基本不等式即可求出cosB的最小值,根据B的范围以及余弦函数的单调性,再利用特殊角三角函数值即可求出B的取值范围,即可判断;
(2)利用三角形的内角的大小,以及三角函数值的大小,结合对数的图象和性质即可判断;
(3)利用a2+c2≥2ac及已知即可证明结论;
(4)由sinA-sinB≤0,利用正弦定理可得a≤b,结合大边对大角即可得解.
解答 解:(1)由a,b,c成等差数列,得到2b=a+c,即b=$\frac{a+c}{2}$,
则cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-(\frac{a+c}{2})^{2}}{2ac}$=$\frac{3({a}^{2}+{c}^{2})-2ac}{8ac}$≥$\frac{6ac-2ac}{8ac}$=$\frac{1}{2}$,
因为B∈(0,π),且余弦函数在(0,π)上为减函数,
所以角B的范围是:0<B≤$\frac{π}{3}$.故为真命题.
(2)若B>$\frac{π}{2}$,则0<sinB<1,A,C为锐角,无法比较sinA,cosC的大小,故结论不一定正确.故为假命题.
(3)因为:a2+c2≥2ac,即a2+c2-ac≥ac,
当b2=ac时,a2+c2-b2≥ac,显然成立,故为真命题.
(4)由sinA-sinB≤0,即:sinA≤sinB,
由正弦定理,sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,
可得:$\frac{a}{2R}$≤$\frac{b}{2R}$,即a≤b,则A≤B,故为真命题.
故答案为:(1)(3)(4).
点评 此题考查学生掌握等差数列的性质,灵活运用余弦定理化简求值,会利用基本不等式求函数的最值,是一道综合题.

| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | {x|-1<x<1且x≠0} | B. | $\left\{x\right.|-1<x<-\frac{1}{2}$或$\frac{1}{2}<x<\left.1\right\}$ | ||
| C. | $\left\{{x|-\frac{1}{2}}\right.<x<\frac{1}{2}$且x≠0} | D. | {x|-1<x<-$\frac{1}{2}$或$0<x<\left.{\frac{1}{2}}\right\}$ |
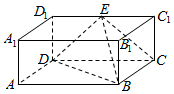 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,