题目内容

7．若x，y满足$\left\{\begin{array}{l}2x-y+2≥0\;\\ x-y+2≥0\;，\;\\ y≥0\;\end{array}\right.$且z=-kx+y有最大值，则k的取值范围为（　　）
A．k≤1B．1≤k≤2C．k≥1D．k≥2

分析 作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合即可得到结论．

解答 解：作出x，y满足$\left\{\begin{array}{l}2x-y+2≥0\;\\ x-y+2≥0\;，\;\\ y≥0\;\end{array}\right.$对应的平面区域如图：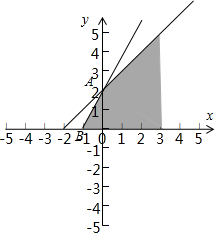

由z=-kx+y得y=kx+z，
∴直线的截距最大，对应的z也取得最大值，
即平面区域在直线y=kx+z的下方，
若k≤0，平移直线y=kx+z，由图象可知，直线在y轴上的截距没有最大值．
如果k≥1，
当直线y=kx+z经过点B或A时，直线y=kx+z的截距最大，
当0＜k＜1，直线在可行域没有满足题意的点．
故选：C．

点评 本题主要考查线性规划的应用，利用z的几何意义，结合数形结合是解决本题的关键．

练习册系列答案
相关题目
17．已知函数f（x）=2sinx，g（x）=2$\sqrt{3}$cosx，直线x=m与f（x），g（x）的图象分别交M，N两点，则|MN|的最大值为4．
18．8个不同的球放入三个相同的盒子中，问有多少种不同的放法？（　　）
A．1094B．966C．5796D．6561
15．如图为一简单几何体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=DA=2，EC=1，N为线段PB的中点．
（Ⅰ）证明：NE⊥PD；
（Ⅱ）求四棱锥B-CEPD的体积．
2．如图，四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PD=CD=2，∠PDC=120°．
（Ⅰ）证明平面PDC⊥平面ABCD；
（Ⅱ）求直线PB与平面ABCD所成角的正弦值．
12．已知函数$f（x）=\frac{{{m^2}x}}{{{x^2}-m}}$，且m≠0．
（Ⅰ）当m=1时，求曲线y=f（x）在点（0，0）处的切线方程；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）若函数f（x）有最值，写出m的取值范围．（只需写出结论）
19．$\frac{sin47°-sin13°}{sin17°}$的值为（　　）
A．$\sqrt{3}$B．1C．-$\sqrt{3}$D．-1
16．一个与自然数有关的命题，若n=k（k∈N）时命题成立可以推出n=k+1时命题也成立．现已知n=10时该命题不成立，那么下列结论正确的是：③（填上所有正确命题的序号）
①n=11时，该命题一定不成立；
②n=11时，该命题一定成立；
③n=1时，该命题一定不成立；
④至少存在一个自然数，使n=n0时，该命题成立．
17．某几何体的三视图如图所示．
（1）画出该几何体的直观图；
（2）求该几何体的表面积和体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网