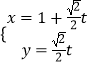Question

【题目】△ABC中，若sinC=（ cosA+sinA）cosB，则（ ）
A.B=
B.2b=a+c
C.△ABC是直角三角形
D.a2=b2+c2或2B=A+C

Answer 1

【答案】D
【解析】解：△ABC中，∵C=π﹣（A+B），∴sinC=sin（A+B），代入sinC=（ cosA+sinA）cosB得，
sin（A+B）=（ cosA+sinA）cosB，
化简可得，cosAsinB= cosAcosB，①
∵0＜A＜π，∴分两种情况讨论，
①当cosA≠0时，①化为sinB= cosB，则tanB= ，
∵0＜B＜π，∴B= ，则A+C=π﹣B= =2B；
②当cosA=0时，A= ，则a2=b2+c2 ，
综上可得，a2=b2+c2或2B=A+C，
故选：D．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:，以及对余弦定理的定义的理解，了解余弦定理:;;．