Question

【题目】已知函数f（x）=sin2wx﹣sin2（wx﹣ ）（x∈R，w为常数且 ＜w＜1），函数f（x）的图象关于直线x=π对称． （I）求函数f（x）的最小正周期；
（Ⅱ）在△ABC中，角A，B，C的对边分别为a，b，c，若a=1，f（ A）= ．求△ABC面积的最大值．

Answer 1

【答案】解：（I）f（x）= cos2ωx﹣[ ﹣ cos（2ωx﹣ ）]= cos（2ωx﹣ ）﹣ cos2ωx=﹣ cos2ωx+ sin2ωx= sin（2ωx﹣ ）． 令2ωx﹣ = +kπ，解得x= ．∴f（x）的对称轴为x= ，
令 =π解得ω= ．∵ ＜w＜1，∴当k=1时，ω= ．
∴f（x）= sin（ x﹣ ）．
∴f（x）的最小正周期T= ．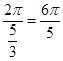
（Ⅱ）∵f（ ）= sin（A﹣ ）= ，∴sin（A﹣ ）= ．∴A= ．
由余弦定理得cosA= = = ．∴b2+c2=bc+1≥2bc，∴bc≤1．
∴S△ABC= = ≤ ．
∴△ABC面积的最大值是
【解析】（1）化简f（x），根据对称轴求出ω，得出f（x）的解析式，利用周期公式计算周期；（2）由f（ A）= 解出A，利用余弦定理和基本不等式得出bc的最大值，代入面积公式得出面积的最大值．