题目内容

【题目】已知方程ln|x|﹣ax2+ =0有4个不同的实数根，則实数a的取值范围是 ．

【答案】
【解析】解：由ln|x|﹣ax2+ =0，得ax2=ln|x|+ ，∵x≠0，
∴方程等价为a= ，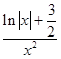
设f（x）= ，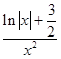
则函数f（x）是偶函数，
当x＞0时，f（x）= ，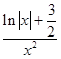
则f′（x）= = ，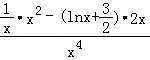
由f′（x）＞0得﹣2x（1+lnx）＞0，得1+lnx＜0，即lnx＜﹣1，得0＜x＜ ，此时函数单调递增，
由f′（x）＜0得﹣2x（1+lnx）＜0，得1+lnx＞0，即lnx＞﹣1，得x＞ ，此时函数单调递减，
即当x＞0时，x= 时，函数f（x）取得极大值f（ ）=
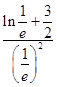
=（﹣1+ ）e2= e2 ，
作出函数f（x）的图象如图：
要使a= ，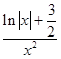
有4个不同的交点，
则满足0＜a＜ ，
所以答案是： ．

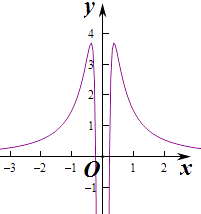
练习册系列答案
相关题目

【题目】已知a∈R，若f（x）=（x+ ﹣1）ex在区间（1，3）上有极值点，则a的取值范围是 ．

【题目】已知数列{an}是公差不为0的等差数列，数列{bn}是等比数列，且b1=a1=1，b2=a3 ， b3=a9
（1）求数列{an}的通项公式；
（2）求数列{anbn}的前n项和Sn ．

【题目】α、β是两个平面，m、n是两条直线，有下列四个命题：
①如果m⊥n ， m⊥α ， n∥β ， 那么α⊥β.
②如果m⊥α ， n∥α ， 那么m⊥n.
③如果α∥β ， m α ， 那么m∥β.
④如果m∥n ， α∥β ， 那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号）

【题目】在单调递增数列{an}中，a1=2，a2=4，且a2n﹣1 ， a2n ， a2n+1成等差数列，a2n ， a2n+1 ， a2n+2成等比数列，n=1，2，3，…．
（Ⅰ）（ⅰ）求证：数列 为等差数列；
（ⅱ）求数列{an}的通项公式．
（Ⅱ）设数列 的前n项和为Sn ， 证明：Sn＞ ，n∈N* ．

【题目】△ABC中，若sinC=（ cosA+sinA）cosB，则（ ）
A.B=
B.2b=a+c
C.△ABC是直角三角形
D.a2=b2+c2或2B=A+C

【题目】在△ABC中，角A，B，C所对的边长分别为a，b，c，且cos = ．
（1）若a=3，b= ，求c的值；
（2）若f（A）=sin （ cos ﹣sin ）+ ，求f（A）的取值范围．

【题目】数列{an}中，a1=1，an﹣an+1=anan+1 ， n∈N* ．
（1）求数列{an}的通项公式；
（2）Sn为{an}的前n项和，bn=S2n﹣Sn ， 求bn的最小值．

【题目】已知f（x）= sinxcosx﹣sin2x，把f（x）的图象向右平移 个单位，再向上平移2个单位，得到y=g（x）的图象，若对任意实数x，都有g（α﹣x）=g（α+x）成立，则g（α+ ）+g（ ）=（ ）
A.4
B.3
C.2
D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网