题目内容
设全集为U=R,集合M={x|3a-1<x<2a,a∈R},N={x|-1<x<3}
(1)若a=0,求M∩N;
(2)若N⊆∁UM,求实数a的取值范围.
(1)若a=0,求M∩N;
(2)若N⊆∁UM,求实数a的取值范围.
考点:集合的包含关系判断及应用,补集及其运算
专题:计算题,集合
分析:(1)若a=0,则M={x|-1<x<0},即可求M∩N;
(2)对集合M进行讨论,然后根据条件N⊆∁UM,即可求实数a的取值范围.
(2)对集合M进行讨论,然后根据条件N⊆∁UM,即可求实数a的取值范围.
解答:
解:(1)若a=0,则M={x|-1<x<0},
∵N={x|-1<x<3},
∴M∩N={x|-1<x<0};
(2)当M=∅,即3a-1≥2a,
∴a≥1时,∁UM=R,满足条件N⊆∁UM,
当M≠∅,即a<1时,∁UM═{x|x≥2a或x≤3a-1},
若N⊆∁UM,
则3a-1≥3或2a≤-1,
即a≥
或a≤-
,此时a≤-
,
综上:a的取值范围是a≤-
或a≥1.
∵N={x|-1<x<3},
∴M∩N={x|-1<x<0};
(2)当M=∅,即3a-1≥2a,
∴a≥1时,∁UM=R,满足条件N⊆∁UM,
当M≠∅,即a<1时,∁UM═{x|x≥2a或x≤3a-1},
若N⊆∁UM,
则3a-1≥3或2a≤-1,
即a≥
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
综上:a的取值范围是a≤-
| 1 |
| 2 |
点评:本题主要考查集合关系的应用,比较基础.要注意对集合M进行分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若球的半径扩大到原来的2倍,那么体积扩大到原来的( )
| A、64倍 | B、16倍 |
| C、8倍 | D、4倍 |
若实数x、y满足
,且x2+y2的最大值等于34,则正实数a的值等于( )
|
A、
| ||
B、
| ||
C、
| ||
| D、3 |
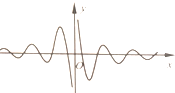 函数y=f(x)的图象如图所示,则f(x)可能是( )
函数y=f(x)的图象如图所示,则f(x)可能是( )| A、xsinx | ||
| B、xcosx | ||
C、
| ||
D、
|
已知直线l1:x+my+6=0与直线l2:(m-2)x+3y+2m=0垂直,则实数m的值为( )
| A、-1 | ||
B、
| ||
| C、3 | ||
| D、2 |
已知函数g(x)=
,则此函数的最小正周期为( )
| ||
|
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
设函数f(x)=sin22x,则f′(x)等于( )
| A、-2cos4x |
| B、-2sin4x |
| C、2cos4x |
| D、2sin4x |