题目内容
5.等比数列{an}前n项和${S_n}=a+{(-\frac{1}{3})^n}$,n∈N*,则$\lim_{n→∞}({a_1}+{a_3}+{a_5}+…+{a_{2n-1}})$=-$\frac{3}{2}$.分析 根据等比数列{an}的前n项和推知a1和q,然后根据求和公式进行计算并求极限.
解答 解:∵等比数列{an}前n项和为Sn=a+(-$\frac{1}{3}$)n,n∈N*,
∴an=Sn-Sn-1=a+(-$\frac{1}{3}$)n-a+(-$\frac{1}{3}$)n-1=-$\frac{4}{3}$•(-$\frac{1}{3}$)n-1,
∴a1=-$\frac{4}{3}$,q=-$\frac{1}{3}$
∴a1,a3,a5,…,a2n-1,为首项-$\frac{4}{3}$,公比为$\frac{1}{9}$的等比数列,
∴a1+a3+a5+…+a2n-1=$\frac{-\frac{4}{3}(1-\frac{1}{{9}^{n}})}{1-\frac{1}{9}}$=-$\frac{3}{2}$(1-$\frac{1}{{9}^{n}}$),
∴$\lim_{n→∞}({a_1}+{a_3}+{a_5}+…+{a_{2n-1}})$=$\underset{lim}{n→∞}$(-$\frac{3}{2}$(1-$\frac{1}{{9}^{n}}$)=-$\frac{3}{2}$
故答案为:$-\frac{3}{2}$
点评 本题考查数列的前2n项中奇数项和的极限的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.设M={x|x=a2+1,a∈R},P={y|y=b2-4b+5,b∈R},则下列关系正确的是( )
| A. | M=P | B. | M?P | ||
| C. | P?M | D. | M与P没有公共元素 |
14.满足条件{2,3}⊆M⊆{1,2,3,4 }的集合M的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
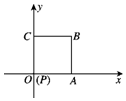 如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.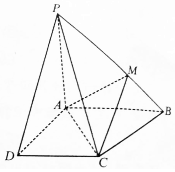 如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠BAD=∠ADC=$\frac{π}{2}$,AB=AD=AP=3,DC=2,点M在PB上,且PM=2MB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠BAD=∠ADC=$\frac{π}{2}$,AB=AD=AP=3,DC=2,点M在PB上,且PM=2MB.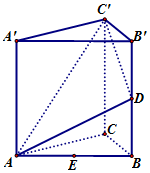 如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上.
如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上.