题目内容
14.已知正实数m,n满足m+n+$\sqrt{{m}^{2}+{n}^{2}}$=2,则mn的最大值为( )| A. | 6-3$\sqrt{2}$ | B. | 2 | C. | 6-4$\sqrt{2}$ | D. | 3 |
分析 根据基本不等式的性质得到$\sqrt{mn}$≤$\frac{2}{2+\sqrt{2}}$,解出即可.
解答 解:∵正实数m,n满足m+n+$\sqrt{{m}^{2}+{n}^{2}}$=2,
∴2$\sqrt{mn}$+$\sqrt{2mn}$≤2,
则(2+$\sqrt{2}$)$\sqrt{mn}$≤2,
故$\sqrt{mn}$≤$\frac{2}{2+\sqrt{2}}$=2-$\sqrt{2}$,
故mn≤${(2-\sqrt{2})}^{2}$=6-4$\sqrt{2}$,
当且仅当m=n时“=“成立,
故选:C.
点评 本题考查了基本不等式的性质,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
19.到两坐标轴的距离相等的轨迹方程是( )
| A. | y=x | B. | y=|x| | C. | x2+y2=0 | D. | y2=x2 |
6.设α,β,γ是三个不重合的平面,m,n是两条不重合的直线,则下列说法正确的是( )
| A. | 若α⊥β,β⊥γ,则α∥γ | B. | 若α⊥β,m∥β,则m⊥α | C. | 若m⊥α,n⊥α,则m∥n | D. | 若m∥α,n∥α,则m∥n |
3.下列命题中错误的是( )
| A. | 命题“?x∈[0,1],使x2-1≥0的否定为“?x∈[0,1],都有x2-1<0” | |
| B. | 命题p为假命题,命题q为真命题,则(¬p)∨(¬q)为真命题 | |
| C. | 命题“若x,y均为奇数,则x+y为奇数”及它的逆命题均为假命题 | |
| D. | 命題“若x2+2x=0,则x=0或x=2”的逆否命题为“若x≠0或x≠2,则x2+2x≠0”. |
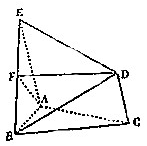 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.