题目内容
16. 如图,已知AB是⊙O的直径,C是⊙O上异于A,B的点,VC垂直于⊙O所在的平面,且AB=4,VC=3.
如图,已知AB是⊙O的直径,C是⊙O上异于A,B的点,VC垂直于⊙O所在的平面,且AB=4,VC=3.(Ⅰ)若点D在△VCB内,且DO∥面VAC,作出点D的轨迹,说明作法及理由;
(Ⅱ)求三棱锥V-ABC体积的最大值,并求取到最大值时,直线AB与平面VAC所成角的大小.
分析 (Ⅰ)取VB,CB的中点,分别记为E,F,连结E,F,由E,F分别为VB、CB的中点,得EF∥VC,从而DO∥面VAC,由此得到D点轨迹是EF.
(Ⅱ)设d为点C到直线AB的距离,由VC⊥面ABC,得到d=2,即C是$\widehat{AB}$的中点时,(VV-ABC)max=4,此时VC⊥BC,AC⊥BC,从而BC⊥面VAC,进而∠CAB是直线AB与面VAC所成的角,由此能求出三棱锥V-ABC体积取到最大值时,直线AB与平面VAC所成角为45°.
解答 解:(Ⅰ)取VB,CB的中点,分别记为E,F,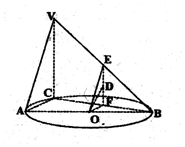
连结E,F,则线段EF即为点D的轨迹,如图所示.
理由如下:
∵E,F分别为VB、CB的中点,
∴EF∥VC,
又EF?面VAC,VC?面VAC,
又D∈EF,OD?面EOF,
∴DO∥面VAC,
∴D点轨迹是EF.
(Ⅱ)设d为点C到直线AB的距离,
∵VC⊥面ABC,
∴${V}_{V-ABC}=\frac{1}{3}×{S}_{△ABC}×VC$
=$\frac{1}{3}×\frac{1}{2}×|AB|×d×|VC|$
=$\frac{1}{6}×4×d×3×2d$,
∵d∈(0,2],∴当d=2,即C是$\widehat{AB}$的中点时,
(VV-ABC)max=4,
∵VC⊥面ABC,BC?面ABC,∴VC⊥BC,
∵AB是⊙O的直径,点C在⊙O上,∴AC⊥BC,
∵AC∩VC=C,∴BC⊥面VAC,
∴AC是AB在面VAC上的射影,
∴∠CAB是直线AB与面VAC所成的角,
∵C是$\widehat{AB}$的中点,
∴CA=CB,∴∠CAB=45°,
∴三棱锥V-ABC体积取到最大值时,直线AB与平面VAC所成角为45°.
点评 本题考查点的轨迹的作法,考查三棱锥的体积的最大值的求法及相应的角的大小的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | 若α⊥β,β⊥γ,则α∥γ | B. | 若α⊥β,m∥β,则m⊥α | C. | 若m⊥α,n⊥α,则m∥n | D. | 若m∥α,n∥α,则m∥n |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |

(Ⅰ)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ=1的概率
(Ⅱ)根据频率分布直方图填写下面2×2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 16 |
| 成绩不优秀 | 38 | 46 | 84 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
| A. | x-2y-4=0 | B. | x-2y+6=0 | C. | x-2y-6=0 | D. | x-2y+4=0 |
| A. | {x|0≤x<3} | B. | {x|1<x≤2} | C. | {x|1<x<3} | D. | {x|x≤2} |
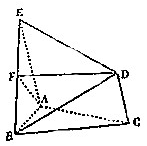 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.