题目内容
7.已知函数f(x)=2|x|,记a=f(log0.53),b=log25,c=f(0),则a,b,c的大小关系为( )| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
分析 利用指数函数、对数函数的单调性求解.
解答 解:函数f(x)=2|x|,记a=f(log0.53),b=log25,c=f(0),
∴a=f(log0.53)=${2}^{|lo{g}_{0.5}3|}$=${2}^{lo{g}_{2}3}$=3,
2=log24<b=log25<log28=3,
c=f(0)=20=1,
∴a,b,c的大小关系为c<b<a.
故选:D.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意指数函数、对数函数的单调性的合理运用.

练习册系列答案
相关题目
15.已知A(-1,0),B是圆F:x2-2x+y2-11=0(F为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为( )
| A. | $\frac{x^2}{12}+\frac{y^2}{11}=1$ | B. | $\frac{x^2}{36}-\frac{y^2}{35}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | D. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ |
19.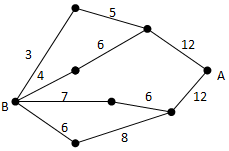 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
16.要排出某班一天中语文、数学、政治、英语、体育、艺术六堂课的课程表,要求数学排在上午(前4节),体育排在下午(后2节),不同排法总数是( )
| A. | 720 | B. | 120 | C. | 144 | D. | 192 |