题目内容
3.过椭圆$M:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$右焦点的直线$x+y-\sqrt{3}=0$交M于A,B两点,P为AB的中点,且OP的斜率为$\frac{1}{2}$,则椭圆M的方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$.分析 由直线方程,代入椭圆方程,求得焦点坐标,利用中点坐标公式及点差法即可求得a和b的关系,又由c=$\sqrt{3}$,即可取得a和b的值,求得椭圆方程.
解答 解:设A(x1,y1),B(x2,y2),P(x0,y0).
直线$x+y-\sqrt{3}=0$过椭圆的焦点,则焦点坐标为($\sqrt{3}$,0),
则x0=$\frac{{x}_{1}+{x}_{2}}{2}$,y0=$\frac{{y}_{1}+{y}_{2}}{2}$,
直线AB的斜率k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=-1.
将A、B代入椭圆方程可得:$\frac{{x}_{1}^{2}}{{a}^{2}}$+$\frac{{y}_{1}^{2}}{{b}^{2}}$=1①,$\frac{{x}_{2}^{2}}{{a}^{2}}$+$\frac{{y}_{2}^{2}}{{b}^{2}}$=1②,
相减可得:①-②得到-$\frac{{b}^{2}}{{a}^{2}}$•$\frac{{y}_{0}}{{x}_{0}}$=-1,
又OP的斜率为$\frac{1}{2}$=$\frac{{y}_{0}}{{x}_{0}}$,
∴a2=2b2,又c=$\sqrt{3}$,a2=b2+c2,
解得a2=6,b2=3.
椭圆的标准方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$.
故答案为:$\frac{x^2}{6}+\frac{y^2}{3}=1$
点评 本题考查椭圆的简单几何性质,利用作差法求椭圆的焦点弦公式,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知f(x)=ax3+bx+5,其中a,b为常数,若f(-9)=-7,则f(9)=( )
| A. | 17 | B. | 7 | C. | 16 | D. | 8 |
14.已知集合A={x|x2-6x+5≤0},B={x|y=log2(x-2)},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
8.执行如图所示的程序框图,若输出结果是5,则输入的整数p的可能性有( )


| A. | 6种 | B. | 7种 | C. | 8种 | D. | 9种 |
12.已知函数f(x)=aex-2x-2a,且a∈[1,2],设函数f(x)在区间[0,ln2]上的最小值为m,则m的取值范围是( )
| A. | [-2,-2ln2] | B. | [-2,-$\frac{1}{e}$] | C. | [-2ln2,-1] | D. | [-1,-$\frac{1}{e}$] |
13.阅读材料:空间直角坐标系O-xyz中,过点P(x0,y0,z0)且一个法向量为$\overrightarrow{n}$=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0;过点P(x0,y0,z0)且个方向向量为$\overrightarrow{d}$=(u,v,w)(uvw≠0)的直线l的方程为$\frac{x-{x}_{0}}{u}$=$\frac{y-{y}_{0}}{v}$=$\frac{z-{z}_{0}}{w}$,阅读上面材料,并解决下面问题:已知平面α的方程为3x-5y+z-7=0,直线l是两个平面x-3y+7=0与4y+2z+1=0的交线,则直线l与平面α所成角的大小为( )
| A. | arcsin$\frac{\sqrt{10}}{35}$ | B. | arcsin$\frac{\sqrt{7}}{5}$ | C. | arcsin$\frac{\sqrt{7}}{15}$ | D. | arcsin$\frac{\sqrt{14}}{55}$ |
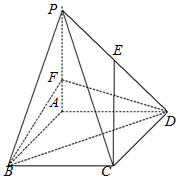 如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.
如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.