题目内容

14．（1）计算：（2-i）（-1+5i）（3+4i）+2i；
（2）已知复数z=（1-i）2+1+3i，若z2+az+b=1-i，a、b∈R，求实数对（a，b）的值．

分析 （1）直接利用复数的代数形式的混合运算化简求解即可求．
（2）化简z2+az+b=1-i，然后利用复数相等列出方程组，即可求实数a，b的值

解答 解：（1）（2-i）（-1+5i）（3+4i）+2i=（3+11i）（3+4i）+2i=-35+45i+2i=-35+47i，
（2）z=（1-i）2+1+3i=-2i+1+3i=1+i，
由z2+az+b=1-i，得（a+b）+（2+a）i=1-i，
∴$\left\{\begin{array}{l}{a+b=1}\\{2+a=-1}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-3}\\{b=4}\end{array}\right.$，
∴实数对（a，b）的值为（-3，4）．

点评 本题考查复数的代数形式的混合运算，复数相等的条件的应用，考查计算能力．

练习册系列答案
相关题目
4．f（x）=$\frac{x^2}{1+x^2}$，求f（$\frac{1}{2}$）+f（$\frac{1}{3}$）+…+f（$\frac{1}{2016}$）+f（2）+f（3）+…+f（2016）
5．若函数f（x），g（x）满足${∫}_{-a}^{a}$f（x）g（x）dx=0（a＞0），则称f（x），g（x）为区间[-a，a]上的一组“垂交函数”．下面给出三组函数：①f（x）=x2-x-2，g（x）=x；②f（x）=sin$\frac{1}{2}$x，g（x）=cos$\frac{1}{2}$x；③f（x）=ex，g（x）=x+1．
其中为区间[-1，1]上的“垂交函数”的组数是（　　）
A．0B．1C．2D．3
2．如果角x的终边在第二象限，那么函数y=$\frac{sinx}{\sqrt{1-co{s}^{2}x}}$+$\frac{cosx}{\sqrt{1-si{n}^{2}x}}$的值为（　　）
A．1B．2C．0D．-1
9．设等差数列{an}的前n项和为Sn，若S6＞S7＞S5，则满足Sn＜0的正整数n的最小值为（　　）
A．12B．13C．14D．15
19．如图，在等腰直角三角形ABC，∠C=90°，点D在线段AB上，且AD=$\frac{1}{3}$AB，延长线段CD至点E，使DE=CD，求cos∠CBE．
6．已知函数f（x）=$\sqrt{3}$sin（$\frac{1}{2}$x+$\frac{π}{6}$）-2cos2（$\frac{1}{4}$x+$\frac{π}{12}$），则不等式f（x）＞0的解集是{x|4kπ+$\frac{π}{3}$＜x＜$\frac{5π}{3}$+4kπ，k∈Z}．
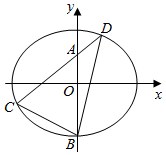3．如图，椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{3}$，点$（\sqrt{3}，\sqrt{2}）$为椭圆上的一点．
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）若斜率为k的直线l过点A（0，1），且与椭圆E交于C，D两点，B为椭圆E的下顶点，求证：对于任意的k，直线BC，BD的斜率之积为定值．
4．如图，在三棱锥A-BCD中，AB⊥平面BCD，BC⊥BD，BC=3，BD=4，直线AD与平面BCD所成的角为45°，点E，F分别是AC，AD的中点．
（1）求证：EF∥平面BCD；
（2）求三棱锥A-BCD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网