题目内容
12.若集合A={x|x(x-3)≤0,x∈N},B={-1,0,1},则集合A∩B为( )| A. | {-1,0} | B. | {1} | C. | {0,1} | D. | {-1,0,1,2,3} |
分析 确定出A,求出A与B的交集即可.
解答 解:集合A={x|x(x-3)≤0,x∈N}={0≤x≤3,x∈N}={0,1,2,3}
B={-1,0,1},
则集合A∩B={0,1}
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
3.双曲线$\frac{y^2}{3}-{x^2}=1$的焦点坐标是( )
| A. | $(±\sqrt{2},0)$ | B. | $(0,±\sqrt{2})$ | C. | (0,±2) | D. | (±2,0) |
20.已知向量$\overrightarrow{a}$=(0,1,1),$\overrightarrow{b}$=(1,2,0),则同时与$\overrightarrow{a}$,$\overrightarrow{b}$垂直的单位向量$\overrightarrow{e}$=( )
| A. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$ | B. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | ||
| C. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | D. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ |
17.已知x=log52,y=ln2,z=${2}^{\frac{1}{2}}$,则下列结论正确的是( )
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
1.已知集合M={x|x2-x-2=0},N={-1,0},则M∩N=( )
| A. | {-1,0,2} | B. | {-1} | C. | {0} | D. | ∅ |
 ,那么这组数据的方差S2可能的最大值是$\frac{164}{5}$.
,那么这组数据的方差S2可能的最大值是$\frac{164}{5}$.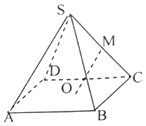 如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.
如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.