题目内容
14．如图函数f（x）的图象在点P处的切线为：y=-2x+5，则f（2）+f′（2）=-1．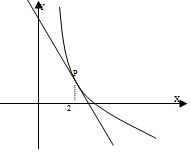
分析 根据导数的几何意义和切线方程求出f′（2），把x=2代入切线方程求出f（2），代入即可求出f（2）+f′（2）的值．
解答 解：∵函数y=f（x）的图象在点x=2处的切线方程是y=-2x+5，
∴f′（2）=-2，f（2）=-4+5=1，
∴f（2）+f′（2）=-2+1=-1，
故答案为：-1
点评 本题考查导数的几何意义，以及切点在切线上的灵活应用，属于基础题．
练习册系列答案
相关题目
4．执行如图所示的程序框图，则输出的S=（ ）
| A． | 4 | B． | 5 | C． | $\sqrt{15}$+1 | D． | 6 |
5．已知全集U=R．集合A={x|x＜3}，B={x|x（x-1）＜0}，则A∩∁UB=（ ）
| A． | {x|1＜x＜3} | B． | {x|x≤0或1≤x＜3} | C． | {x|x＜3} | D． | {x|1≤x＜3} |
9．计算定积分${∫}_{0}^{2π}$|cosx|dx的值为（ ）
| A． | 0 | B． | 2 | C． | 4 | D． | -4 |
6．设i是虚数单位，复数z满足z•（1+2i）2=3+4i，则z在复平面内对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
已知某四棱锥的三视图如图所示，则该几何体的各侧面中，面积的最小值为$\frac{1}{2}$．
4．若两个不同平面α、β的法向量分别为$\overrightarrow{u}$=（1，2，-1），$\overrightarrow{v}$=（-2，2，2），则（ ）
| A． | α、β相交但不垂直 | B． | α⊥β | C． | α∥β | D． | 以上均不正确 |