题目内容
12.在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1,F2分别为椭圆G$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左、右焦点,A为椭圆G的左顶点,已知△F1PF2为等腰三角形.(Ⅰ)求椭圆G的离心率;
(Ⅱ)过F2的直线m:x=1与椭圆G相交于点M(M点在第一象限),平行于AM的直线l与椭圆G交于B,C两点,判断直线MB,MC是否关于直线m对称,并说明理由.
分析 (Ⅰ)由a>b,可得PF1=F1F2,或PF2=F1F2,设F1(-c,0),F2(c,0),运用两点的距离公式和离心率公式,计算即可得到所求值;
(Ⅱ)由已知条件得椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,即有A(-2,0),M(1,$\frac{3}{2}$),设直线l:y=$\frac{1}{2}$x+n,n≠1.设B(x1,y1),C(x2,y2),由 $\left\{\begin{array}{l}{y=\frac{1}{2}x+n}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,得x2+nx+n2-3=0.再由根的判别式和韦达定理结合已知条件能求出直线MB,MC关于直线m对称.
解答 解:(Ⅰ)由a>b,可得PF1≠PF2,
设F1(-c,0),F2(c,0),若PF1=F1F2,
则$\sqrt{(a+c)^{2}+{b}^{2}}$=2c,即有a2+ac-2c2=0,①
由a<c,可得a2+ac<2c2,故方程①无解;
若PF2=F1F2,
则$\sqrt{(a-c)^{2}+{b}^{2}}$=2c,即有a2-ac-2c2=0,
即有2e2+e-1=0,解得e=$\frac{1}{2}$(1舍去),
综上可得,椭圆G的离心率为$\frac{1}{2}$;
(Ⅱ)由F2(1,0),可得c=1,a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
∵A为椭圆G的左顶点,∴A(-2,0),M(1,$\frac{3}{2}$),
∴由题意可设直线l:y=$\frac{1}{2}$x+n,n≠1.
设B(x1,y1),C(x2,y2),
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+n}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,得x2+nx+n2-3=0.
由题意得△=n2-4(n2-3)=12-3n2>0,
即n∈(-2,2)且n≠1.
x1+x2=-n,x1x2=n2-3.
∵kMB+kMC=kMB+kMC=$\frac{{y}_{1}-\frac{3}{2}}{{x}_{1}-1}$+$\frac{{y}_{2}-\frac{3}{2}}{{x}_{2}-1}$=$\frac{\frac{1}{2}{x}_{1}+n-\frac{3}{2}}{{x}_{1}-1}$+$\frac{\frac{1}{2}{x}_{2}+n-\frac{3}{2}}{{x}_{2}-1}$
=1+$\frac{n-1}{{x}_{1}-1}$+$\frac{n-1}{{x}_{2}-1}$=1+$\frac{(n-1)({x}_{1}+{x}_{2}-2)}{{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1}$
=1-$\frac{(n-1)(n+2)}{{n}^{2}+n-2}$=0,
故直线MB,MC关于直线m对称.
点评 本题考查椭圆方程的求法,考查两条直线是否关于已知直线对称的判断,解题时要认真审题,注意根的判别式和韦达定理的合理运用.

| A. | 向左平移$\frac{π}{8}$个单位长度 | B. | 向右平移$\frac{π}{8}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
| A. | f(f(x))=(f(x))2 | B. | f(f(x))=f(x) | C. | f(f(x))>f(x) | D. | f(f(x))<f(x) |
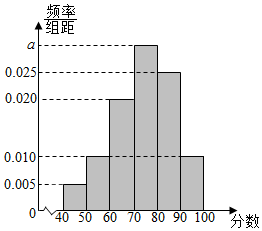 某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图. 如图所示,E,F分别是正方体ABCD-A1B1C1D1中BB1,B1C1的中点,计算:
如图所示,E,F分别是正方体ABCD-A1B1C1D1中BB1,B1C1的中点,计算: