已知集合A={x||x|≤2}.B={x|x2-x-2＜0}.则A∩∁RB=( )A．RB．{x|-2≤x≤-1}C．{x|-2≤x≤-1或x＞2}D．{x|-2≤x≤-1或x=2} 题目和参考答案——青夏教育精英家教网—

题目内容

20．已知集合A={x||x|≤2}，B={x|x²-x-2＜0}，则A∩∁_RB=（　　）

A．

B．

{x|-2≤x≤-1}

C．

{x|-2≤x≤-1或x＞2}

D．

{x|-2≤x≤-1或x=2}

分析解不等式得出集合A、B，根据补集与交集的定义写出A∩∁_RB即可．

解答解：集合A={x||x|≤2}={x|-2≤x≤2}，
B={x|x²-x-2＜0}={x|-1＜x＜2}，
∴∁_RB={x|x≤-1或x≥2}，
∴A∩∁_RB={x|-2≤x≤-1或x=2}．
故选：D．

点评本题考查了解不等式和补集与交集的运算问题，是基础题．

练习册系列答案

11．已知F₁、F₂分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，离心率为$\frac{\sqrt{3}}{3}$，点P在椭圆C上，且点P在x轴上的正投影恰为F₁，在y轴上的正投影为点（0，$\frac{2\sqrt{3}}{3}$）．
（1）求椭圆C的方程；
（2）过点F₁且倾斜角为$\frac{5π}{6}$的直线l与椭圆C交于A，B两点，过点P且平行于直线l的直线交椭圆C于另一点Q，求证：四边形PABQ为平行四边形．

8．已知f（x）=$\left\{\begin{array}{l}{-2{x}^{2}+3x，-2≤x＜0}\\{ln\frac{1}{x+1}，0≤x≤2}\end{array}\right.$，若g（x）=|f（x）|-ax-a的图象与x轴有3个不同的交点，则实数a的取值范围为（　　）

A．

[$\frac{ln3}{3}$，$\frac{1}{e}$）

B．

[$\frac{ln3}{3}$，$\frac{1}{2e}$]

15．命题p：将函数y=cosx•sinx的图象向右平移$\frac{3π}{4}$个单位可得到y=$\frac{1}{2}$cos2x的图象；命题q：对?m＞0，双曲线2x²-y²=m²的离心率为$\sqrt{3}$，则下列结论正确的是（　　）

5．△ABC中，角A、B、C的对边分别为a、b、c，G是平面△ABC上一点，且满足a•$\overrightarrow{GA}$+b•$\overrightarrow{GB}$+c•$\overrightarrow{GC}$=0，则G是△ABC中的（　　）

12．变量x，y满足约束条件$\left\{\begin{array}{l}x-y≤0\\ y≤10-2x\\ x-1≥0\end{array}$，则z=2x-y的最小值为-6．

9．

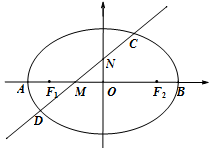如图，椭圆E的左右顶点分别为A、B，左右焦点分别为F₁、F₂，|AB|=4，|F₁F₂|=2$\sqrt{3}$，直线l：y=kx+m（k＞0）交椭圆于C、D两点，与线段F₁F₂及椭圆短轴分别交于M、N两点（M、N不重合），且|CM|=|DN|．
（Ⅰ）求椭圆E的离心率；
（Ⅱ）若CD的垂直平分线过点（-1，0），求直线l的方程．

10．已知i为虚数单位，z（1-i）=1+i，则复数z的共轭复数为（　　）

试题分类