题目内容
已知在△ABC中，a=7，b=10，c=6，则此三角形为（ ）
| A、钝角三角形 | B、锐角三角形 |
| C、直角三角形 | D、不确定 |
考点：余弦定理
专题：计算题,解三角形
分析：利用余弦定理，计算cosB，即可得出结论．
解答：
解：∵a=7，b=10，c=6，
∴cosB=
=-
＜0，
∴B为钝角，
∴三角形为钝角三角形．
故选：A．
∴cosB=
| 72+62-102 |
| 2×7×6 |
| 5 |
| 28 |
∴B为钝角，
∴三角形为钝角三角形．
故选：A．
点评：本题考查余弦定理，考查三角形形状的判断，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
sin75°=（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列函数中，在区间（-1，1）上是减函数的是（ ）
| A、y=2-3x2 | ||
| B、y=lnx | ||
C、y=
| ||
| D、y=sinx |
下列说法错误的是（ ）
| A、若“p且q”为假命题，则p、q至少有一个为假命题 | ||||||||||||||||
B、若
| ||||||||||||||||
| C、命题“若x2-3x+2=0，则x=1”的逆否命题为：“x≠1，则x2-3x+2≠0” | ||||||||||||||||
| D、命题p：“?x∈R，使得x2+x+1＜0”，则￢p：“?x∈R，均有x2+x+1≥0” |
已知f（x）=
，则下列叙述中不正确的一项是（ ）
|
A、 f（x-1）的图象 |
B、 |f（x）|的图象 |
C、 f（-x）的图象 |
D、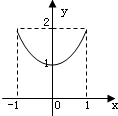 f（|x|）的图象 |
下列不等式对任意的x∈（0，+∞）恒成立的是（ ）
| A、sinx＞-x+1 |
| B、x-x2＞0 |
| C、x＞ln（1+x） |
| D、e2＞ex |
设集合A={x|-3≤x≤0}，B={x|-1≤x≤3}，则A∩B=（ ）
| A、[-1，0] |
| B、[-3，3] |
| C、[0，3] |
| D、[-3，-1] |
已知x∈[0，2π]，如果y=cosx是减函数，且y=sinx是增函数，那么（ ）
A、0≤x≤
| ||
B、
| ||
C、π≤x≤
| ||
D、
|