题目内容
若一物体运动方程如下(位移:m,时间:s)
s=
求:(1)物体在t∈[3,5]内的平均速度;
(2)物体的初速度V0;
(3)物体在t=1时的瞬时速度.
s=
|
求:(1)物体在t∈[3,5]内的平均速度;
(2)物体的初速度V0;
(3)物体在t=1时的瞬时速度.
考点:分段函数的应用,导数的几何意义,导数的运算
专题:计算题,函数的性质及应用,导数的概念及应用
分析:(1)计算时间变化量为△t=2,其位移变化量为△s=s(5)-s(3),即可求出物体在t∈[3,5]内的平均速度;
(2)化简t∈[0,3)内的位移,结合物体做匀变速直线运动的公式,即可得到初速度;
(3)求出速度增量,即可得出物体在t=1时的瞬时速度.
(2)化简t∈[0,3)内的位移,结合物体做匀变速直线运动的公式,即可得到初速度;
(3)求出速度增量,即可得出物体在t=1时的瞬时速度.
解答:
解:(1)由已知在t∈[3,5]时,其时间变化量为△t=2,
其位移变化量为△s=s(5)-s(3)=3×25+2-(3×9+2)=48,
故所求平均速度为
=
=24m/s;
(2)当0≤t<3时,s=29+3(t-3)2=3t2-18t+56,
由物体做匀变速直线运动的位移公式,可得物体的初速度V0为-18m/s;
(3)
=
=
=3△t-12,
故物体在t=1时的瞬时速度为
=
(3△t-12)=-12m/s.
其位移变化量为△s=s(5)-s(3)=3×25+2-(3×9+2)=48,
故所求平均速度为
| △s |
| △t |
| 48 |
| 2 |
(2)当0≤t<3时,s=29+3(t-3)2=3t2-18t+56,
由物体做匀变速直线运动的位移公式,可得物体的初速度V0为-18m/s;
(3)
| △s |
| △t |
| s(1+△t)-s(1) |
| △t |
| 29+3(1+△t-3)2-29-3(1-3)2 |
| △t |
故物体在t=1时的瞬时速度为
| lim |
| △t→0 |
| △s |
| △t |
| lim |
| △t→0 |
点评:本题考查分段函数的应用,主要考查平均速度、初速度和瞬时速度的求法,考查导数的概念及应用,比较基础.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列几何体中不是旋转体的是( )
A、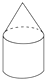 |
B、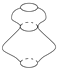 |
C、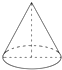 |
D、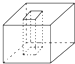 |
如果圆柱与圆锥的底面直径、高和球的直径相等,则体积比V圆柱:V圆锥:V球为( )
| A、3:1:2 | ||
| B、3:1:4 | ||
C、6:
| ||
| D、3:3:2 |
已知MP、OM、AT分别是60°角的正弦线、余弦线、正切线,如图,则一定有( )
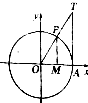

| A、MP<OM<AT |
| B、AT<OM<MP |
| C、OM<MP<AT |
| D、OM<AT<MP |
下表为某大型超市一个月的销售收入情况表,则本月销售收入的平均增长率( )
| 日期 | 5 | 10 | 15 | 20 | 25 | 30 |
| 销售收入(万元) | 20 | 40 | 90 | 160 | 275 | 437.5 |
| A、一样 | B、越来越大 |
| C、越来越小 | D、无法确定 |