题目内容
15.C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$等于( )| A. | C${\;}_{21}^{17}$ | B. | C${\;}_{21}^{17}$-1 | C. | C${\;}_{21}^{18}$-1 | D. | C${\;}_{21}^{18}$ |
分析 利用组合数的性质求解即可.
解答 解:C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$=1+C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$-1
=${C}_{4}^{0}$+C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$-1
=${C}_{5}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$-1
=${C}_{6}^{2}$+C${\;}_{6}^{3}$+…+C${\;}_{20}^{17}$-1
=…
=C${\;}_{21}^{17}$-1.
故选:B.
点评 本题考查组合数性质的应用,考查计算能力.

练习册系列答案
相关题目
6.某城市现有人口100万,根据最近20年的统计资料,这个城市的人口的年自然增长率为1.2%,按这个增长计算10年后这个城市的人口预计有( )万.
| A. | y=100×0.01210 | B. | y=100×(1+1.2%)10 | C. | y=100×(1-1.2%)10 | D. | y=100×1.210 |
10.“m=1”是“函数f(x)=log2(1+mx)+log2(1-x)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
(Ⅰ)若“身高大于175厘米”的为“高个”,“身高不超过175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长不超过42码”的为“非大脚”.
请根据上表数据完成下面的2×2列联表:
(Ⅱ)根据(1)中表格的数据,你能否有99%的把握认为脚的大小与身高有关系?
K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(cm) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 49 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(cm) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 42 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
请根据上表数据完成下面的2×2列联表:
| 高个 | 非高个 | 合计 | |
| 大脚 | |||
| 非大脚 | 12 | ||
| 合计 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
14.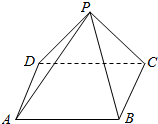 已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
 已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |