题目内容
13.某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(cm) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 49 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(cm) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 42 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
请根据上表数据完成下面的2×2列联表:
| 高个 | 非高个 | 合计 | |
| 大脚 | |||
| 非大脚 | 12 | ||
| 合计 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)根据高个和大脚的描述,统计出大脚,高个,非大脚和非高个的数据,填入列联表,再在合计的部分填表.
(2)提出假设,代入公式做出观测值,把所得的观测值同表格中的临界值进行比较,可得绪论.
解答 解:(1)根据“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;
“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,统计出数据
列联表为:
| 高个 | 非高个 | 合计 | |
| 大脚 | 5 | 2 | 7 |
| 非大脚 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
(2)提出假设H0:人的脚的大小与身高之间没有关系,
根据上述列联表可以求得K2=$\frac{20(5×12-1×2)^{2}}{6×14×13×7}$≈8.802,
∵8.802>6.635,
所以我们有99%的把握认为:人的脚的大小与身高之间有关系…(12分)
点评 本题考查独立性检验,包括数据的统计,是一个基础题,本题在个别省份作为高考题目出现过,要引起同学们注意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$等于( )
| A. | C${\;}_{21}^{17}$ | B. | C${\;}_{21}^{17}$-1 | C. | C${\;}_{21}^{18}$-1 | D. | C${\;}_{21}^{18}$ |
5.当x→0时,下列四个无穷小阶数最高的是( )
| A. | e${\;}^{{x}^{4}-{x}^{3}}$-1 | B. | cosx2-1 | C. | $\sqrt{1+{x}^{2}}$-1 | D. | tanx-sinx |
2.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1B上一动点,则AP+D1P的最小值为( )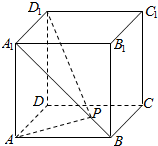

| A. | 2 | B. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{2+\sqrt{2}}$ |
