题目内容
3.函数y=$\frac{{x}^{2}-4x+13}{x-1}$(x∈[2,5])的值域为[2$\sqrt{10}$-2,9].分析 首先将函数化为:y=(x-1)+$\frac{10}{x-1}$-2,再用基本不等式和双勾函数的性质求最值.
解答 解:y=f(x)=$\frac{{x}^{2}-4x+13}{x-1}$=$\frac{(x-1)^2-2(x-1)+10}{x-1}$=(x-1)+$\frac{10}{x-1}$-2,
∵x∈[2,5],∴x-1∈[1,4],
根据基本不等式,(x-1)+$\frac{10}{x-1}$≥2$\sqrt{(x-1)•\frac{10}{x-1}}$=2$\sqrt{10}$,
当且仅当:(x-1)=$\frac{10}{x-1}$,解得x=$\sqrt{10}$+1∈[2,5],
所以,ymin=2$\sqrt{10}$-2,
再根据双勾函数的性质,ymax=max{f(2),f(5)},
其中,f(2)=9,f(5)=$\frac{9}{2}$,所以ymax=9,
所以该函数的值域为:[2$\sqrt{10}$-2,9].
故答案为:[2$\sqrt{10}$-2,9].
点评 本题主要考查了函数值域的求法,涉及双勾函数的性质,以及运用基本不等式最值,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
15.C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$等于( )
| A. | C${\;}_{21}^{17}$ | B. | C${\;}_{21}^{17}$-1 | C. | C${\;}_{21}^{18}$-1 | D. | C${\;}_{21}^{18}$ |
2.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1B上一动点,则AP+D1P的最小值为( )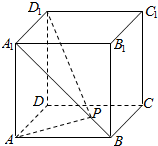

| A. | 2 | B. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{2+\sqrt{2}}$ |