题目内容
6.在△ABC中,内角A,B,C的对边分别为a,b,c,已知$c=2,C=\frac{π}{3}$.(1)若$a=\frac{{2\sqrt{3}}}{3}$,求A;
(2)若sinB=2sinA,求△ABC的面积.
分析 (1)由正弦定理可得:$\frac{\frac{2\sqrt{3}}{3}}{sinA}$=$\frac{2}{sin\frac{π}{3}}$,解得sinA=$\frac{1}{2}$,又a<c,则A为锐角,解得A.
(2)sinB=2sinA,由正弦定理可得b=2a,又22=a2+b2-2abcos$\frac{π}{3}$,解得a,b.可得△ABC的面积S=$\frac{1}{2}absinC$.
解答 解:(1)由正弦定理可得:$\frac{\frac{2\sqrt{3}}{3}}{sinA}$=$\frac{2}{sin\frac{π}{3}}$,解得sinA=$\frac{1}{2}$,又a<c,则A为锐角,A∈$(0,\frac{π}{2})$,∴A=$\frac{π}{6}$.
(2)sinB=2sinA,由正弦定理可得b=2a,又22=a2+b2-2abcos$\frac{π}{3}$,解得a=$\frac{2\sqrt{3}}{3}$,b=$\frac{4\sqrt{3}}{3}$.
∴△ABC的面积S=$\frac{1}{2}absinC$=$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×$\frac{4\sqrt{3}}{3}$×$sin\frac{π}{3}$=$\frac{2\sqrt{3}}{3}$..
点评 本题考查了正弦定理余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
17.从集合{0,1,2,3,4,5}中任取两个互不相等的数x,y组成复数z=x+yi,其中虚数的个数有( )
| A. | 5 | B. | 30 | C. | 25 | D. | 36 |
14.菱形ABCD中,AC=2,则$\overrightarrow{AC}•\overrightarrow{AD}$=( )
| A. | $-\frac{3}{2}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | 2 |
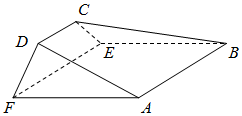 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为矩形,AF⊥DF,且二面角D-AF-E与二面角C-BE-F都等于$α(0<α<\frac{π}{2})$.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为矩形,AF⊥DF,且二面角D-AF-E与二面角C-BE-F都等于$α(0<α<\frac{π}{2})$.