题目内容

14．菱形ABCD中，AC=2，则$\overrightarrow{AC}•\overrightarrow{AD}$=（　　）
A．$-\frac{3}{2}$B．-3C．$\frac{1}{2}$D．2

分析 根据向量的数量积公式计算即可．

解答 解：因为$\overrightarrow{AC}•\overrightarrow{AD}=|{\overrightarrow{AC}}||{\overrightarrow{AD}}|cos∠CAD=\frac{1}{2}{|{\overrightarrow{AC}}|^2}=2$，
故选D．

点评 本题考查向量数量积的概念与计算，注意结合菱形的对角线的性质．

练习册系列答案
相关题目
4．在等差数列{an}中，若a2=4，a4=2，则a6=0．
5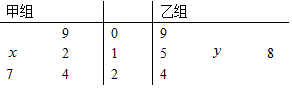．如图茎叶图记录了甲．乙两组各五名学生在一次英语听力测试中的成绩（单位：分）已知甲组数据的中位数为5，乙组数据的平均数为6.8，则x，y的值分别为（　　）
A．2，5B．5，5C．5，8D．8，8
2．已知集合A={1，2，3}，B={x|2≤x≤5}，则集合A∩B为{2，3}．
9．已知{an}满足${a_1}=1，{a_n}+{a_{n+1}}={（{\frac{1}{4}}）^n}（{n∈{N^*}}），{S_n}={a_1}+4•{a_2}+{4^2}•{a_3}+…+{4^{n-1}}{a_n}$，类比课本中推导等比数列前n项和公式的方法，可求得${S_n}-\frac{4^n}{5}{a_n}$=$\frac{n}{5}$．
19．设$a={2^{\frac{1}{3}}}，b={log_4}3，c={log_8}5$，则（　　）
A．a＞b＞cB．a＞c＞bC．c＞a＞bD．b＞c＞a
6．在△ABC中，内角A，B，C的对边分别为a，b，c，已知$c=2，C=\frac{π}{3}$．
（1）若$a=\frac{{2\sqrt{3}}}{3}$，求A；
（2）若sinB=2sinA，求△ABC的面积．
3．下面说法不正确的选项（　　）
A．函数的单调区间可以是函数的定义域
B．函数的多个单调增区间的并集也是其单调增区间
C．具有奇偶性的函数的定义域定关于原点对称
D．关于原点对称的图象一定是奇函数的图象
4．若a表示“向东走8km”，b表示“向北走8km”，则a+b表示向东北方向走8$\sqrt{2}$km．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网