题目内容
15.已知△ABC的三个顶点坐标分别为A(-2,4),B(-1,1),C(3,3).(1)求边BC的垂直平分线的方程;
(2)求△ABC的面积.
分析 (1)线段BC的中点D的坐标为(1,2),利用斜率计算公式可得:直线的BC斜率kBC,进而定点边BC的垂直平分线的斜率为-$\frac{1}{{k}_{BC}}$,利用点斜式即可得出.
(2)利用两点之间的距离公式、点到直线的距离公式即可得出.
解答 解:(1)线段BC的中点D的坐标为(1,2),
又直线的BC斜率为${k_{BC}}=\frac{3-1}{3+1}=\frac{1}{2}$,
∴边BC的垂直平分线的斜率为-2,
故边BC的垂直平分线的方程为y-2=-2(x-1),即2x+y-4=0.
(2)$|{BC}|=\sqrt{[{3-{{({-1})}^2}}]+{{({3-1})}^2}}=2\sqrt{5}$,
直线BC的方程是$y-1=\frac{1}{2}({x+1})$,即x-2y+3=0,
点A到直线BC的距离$d=\frac{{|{-2-2×4+3}|}}{{\sqrt{{1^2}+{{({-2})}^2}}}}=\frac{7}{{\sqrt{5}}}$,
∴△ABC的面积$S=\frac{1}{2}|{BC}|•d=\frac{1}{2}×2\sqrt{5}×\frac{7}{{\sqrt{5}}}=7$.
点评 本题考查了直线的方程、两点之间的距离公式、点到直线的距离公式、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
5.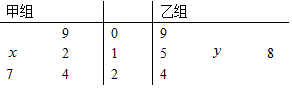 如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )
如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )
 如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )
如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )| A. | 2,5 | B. | 5,5 | C. | 5,8 | D. | 8,8 |
3.下面说法不正确的选项( )
| A. | 函数的单调区间可以是函数的定义域 | |
| B. | 函数的多个单调增区间的并集也是其单调增区间 | |
| C. | 具有奇偶性的函数的定义域定关于原点对称 | |
| D. | 关于原点对称的图象一定是奇函数的图象 |
20.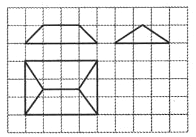 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )| A. | 5000立方尺 | B. | 5500立方尺 | C. | 6000立方尺 | D. | 6500立方尺 |
5.复平面上三点A、B、C分别对应复数1,2i,5+2i,则由A,B,C为顶点所构成的三角形是( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 直角三角形 |