△ABC中.∠A=90°.AC=2.D为边BC的中点.则$\overrightarrow{AD}•\overrightarrow{AC}$=2．题目和参考答案——青夏教育精英家教网——

题目内容

1．△ABC中，∠A=90°，AC=2，D为边BC的中点，则$\overrightarrow{AD}•\overrightarrow{AC}$=2．

分析根据向量的数量积的运算法则计算即可．

解答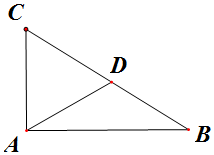解：△ABC中，∠A=90°，AC=2，D为边BC的中点，
则$\overrightarrow{AD}•\overrightarrow{AC}$=$\frac{1}{2}$（$\overrightarrow{AC}$+$\overrightarrow{AB}$）•$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AC}$²+$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{1}{2}$×2²=2，
故答案为：2．

点评本题考查了向量的数量积的运算，属于基础题．

练习册系列答案

晨光全优口算应用题天天练系列答案

提优检测卷初中强化拓展系列答案

百渡中考必备中考试题精选系列答案

魅力语文系列答案

状元龙初中语文现代文阅读系列答案

初中现代文文言文拓展阅读系列答案

启光中考全程复习方案系列答案

授之以渔中考试题汇编系列答案

中考前沿系列答案

宇轩图书小学毕业升学系统总复习系列答案

相关题目

11．变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ x-2y≤0\\ x+y≥3\end{array}\right.$，则x²+y²的取值范围是（　　）

$[\frac{{3\sqrt{2}}}{2}，+∞）$

$[\frac{9}{2}，+∞）$

12．在△ABC中，角A，B，C对应的边分别是a，b，c，已知cos2C-3cos（A+B）=1．
（1）求C；
（2）若c=$\sqrt{7}$，b=3a，求△ABC的面积．

9．已知{a_n}满足${a_1}=1，{a_n}+{a_{n+1}}={（{\frac{1}{4}}）^n}（{n∈{N^*}}），{S_n}={a_1}+4•{a_2}+{4^2}•{a_3}+…+{4^{n-1}}{a_n}$，类比课本中推导等比数列前n项和公式的方法，可求得${S_n}-\frac{4^n}{5}{a_n}$=$\frac{n}{5}$．

16．已知点P为不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.$所表示的平面区域内的一点，点Q是圆M：（x+1）²+y²=1上的一个动点，则|PQ|的最大值是（　　）

$\frac{{3\sqrt{5}+2}}{2}$

$\frac{{2\sqrt{5}+3}}{3}$

$\frac{{2\sqrt{5}}}{3}$

6．在△ABC中，内角A，B，C的对边分别为a，b，c，已知$c=2，C=\frac{π}{3}$．
（1）若$a=\frac{{2\sqrt{3}}}{3}$，求A；
（2）若sinB=2sinA，求△ABC的面积．

13．已知x满足不等式${log_{\frac{1}{2}}}{x^2}$≥${log_{\frac{1}{2}}}（3x-2）$，函数$f（x）=（{log_2}\frac{x}{4}）（{log_2}\frac{x}{2}）$．
（Ⅰ）求出x的取值范围；
（Ⅱ）求f（x）的值域．

10．设函数$f（x）=（{x-1}）{e^{x-1}}+\frac{a}{2}{x^2}$．
（1）讨论函数f（x）的单调性；
（2）若a≥-e，讨论函数f（x）的零点的个数．

11．设抛物线C：y²=2px（p＞0）过点$M（2，-2\sqrt{2}）$．
（Ⅰ）求抛物线C的方程；
（Ⅱ）过点F（1，0）作相互垂直的两条直线l₁，l₂，曲线C与l₁交于点P₁，P₂，与l₂交于点Q₁，Q₂．证明：$\frac{1}{{|{{P_1}{P_2}}|}}+\frac{1}{{|{{Q_1}{Q_2}}|}}=\frac{1}{4}$；
（Ⅲ）在（Ⅱ）中，我们得到关于抛物线的一个优美结论．请你写出关于椭圆$Γ：\frac{x^2}{4}+\frac{y^2}{3}=1$的一个相类似的结论（不需证明）．