题目内容

17．已知直线x-y-2=0与曲线x2-y2=4m的交点P在圆（x-4）2+y2=4的内部，则实数m的取值范围是（　　）
A．-1＜m＜3B．-3＜m＜-1C．1＜m＜3D．2＜m＜3

分析 求出直线与双曲线的交点坐标，以及圆的圆心的距离小于半径，求解即可．

解答 解：由题意可知：$\left\{\begin{array}{l}x-y-2=0\\{x}^{2}{-y}^{2}=4m\end{array}\right.$，解得$\left\{\begin{array}{l}x=m+1\\ y=m-1\end{array}\right.$，交点（m+1，m-1），
交点P在圆（x-4）2+y2=4的内部，
可得（m-3）2+（m-1）2＜4，
解得1＜m＜3．
故选：C．

点评 本题考查直线与双曲线的位置关系，点与圆的位置关系的应用，考查计算能力．

练习册系列答案
相关题目
7．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，连接椭圆四个顶点形成的四边形面积为4$\sqrt{2}$，求椭圆C的标准方程．
8．设斜率为k（k≠0）的直线与离心率为$\frac{\sqrt{2}}{2}$的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）相交于A、B两点，P是线段AB的中点，直线OP的斜率为k′．
（Ⅰ）证明积kk′是定值；
（Ⅱ）若直线0P的倾斜角为$\frac{3π}{4}$时△OAB面积的最大值为$\frac{\sqrt{2}}{2}$，求椭圆的方程．
5．在平面直角坐标系xOy中，已知两点E（-1，0）和F（1，0），动点M满足$\overrightarrow{EM}•\overrightarrow{FM}$=0，设点M的轨迹为C，半抛物线C′：y2=2x（y≥0），设点$D（\frac{1}{2}\;，\;0）$．
（Ⅰ）求C的轨迹方程；
（Ⅱ）设点T是曲线C′上一点，曲线C′在点T处的切线与曲线C相交于点A和点B，求△ABD的面积的最大值及点T的坐标．
12．某人一次同时抛掷两枚均匀骰子（它们的六个面分别标有点数1、2、3、4、5、6）求：
（1）两枚骰子点数相同的概率；
（2）两枚骰子点数和为5的倍数的概率．
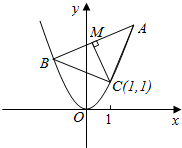2．过抛物线y=x2上定点C（1，1）引两条互相垂直的弦CA、CB，作CM⊥AB，M为垂足，求点M的轨迹方程．
9．设曲线y=3x-ln（x+a）在点（0，0）处的切线方程为y=2x，则a=（　　）
A．0B．1C．2D．3
6．已知函数f（x）=$\left\{\begin{array}{l}{log_2}（-x），\;\;x＜0\\{3^{x-1}}，\;\;\;\;\;\;\;\;\;\;x≥0\end{array}$，则f（1）=1，f（-6）=log26．
7．已知F1，F2分别是离心率为$\frac{3}{5}$的椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点，P为椭圆E上一点，且△F1F2P的周长为16．
（1）求椭圆E的方程；
（2）若|PF1|=$\frac{16}{5}$，求点P到椭圆左顶点A的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网