题目内容
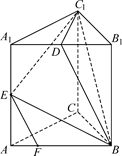
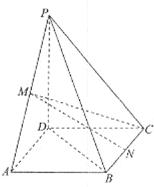
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=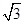 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.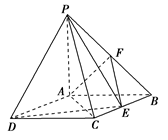
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有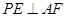 ;
;
(3)当 为何值时,
为何值时,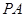 与平面
与平面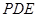 所成角的大小为45°.
所成角的大小为45°.
(1)EF//面PAC (2)因PA⊥底面ABCD,所以DA⊥PA,又DA⊥AB,所以DA⊥面PAB,又DA//CB,所以CB⊥面PAB所以 ,因为AF⊥PB所以AF⊥面PBC有
,因为AF⊥PB所以AF⊥面PBC有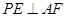 (3)
(3)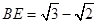
解析试题分析:⑴当E是BC中点时,因F是PB的中点,所以EF为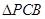 的中位线,
的中位线,
故EF//PC,又因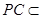 面PAC,
面PAC,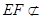 面PAC,所以EF//面PAC 4分
面PAC,所以EF//面PAC 4分
⑵证明:因PA⊥底面ABCD,所以DA⊥PA,又DA⊥AB,所以DA⊥面PAB,
又DA//CB,所以CB⊥面PAB,而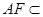 面PAB,所以
面PAB,所以 ,
,
又在等腰三角形PAB中,中线AF⊥PB,PB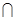 CB=B,所以AF⊥面PBC.
CB=B,所以AF⊥面PBC.
而PE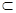 面PBC,所以无论点E在BC上何处,都有
面PBC,所以无论点E在BC上何处,都有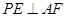 8分
8分
⑶以A为原点,分别以AD、AB、AP为x\y\z轴建立坐标系,设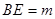 ,
,
则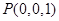 ,
,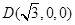 ,
,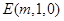 ,设面PDE的法向量为
,设面PDE的法向量为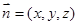 ,
,
由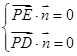 ,得
,得 ,取
,取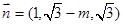 ,又
,又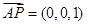 ,
,
则由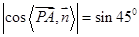 ,得
,得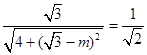 ,解得
,解得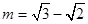 .
.
故当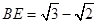 时,PA与面PDE成
时,PA与面PDE成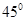 角 12分
角 12分
考点:线面平行垂直的判定及线面角的求解
点评:证明线面平行时常借助于已知的中点转化为线线平行,第三问求线面角采用空间向量的方法思路较简单,只需求出直线的方向向量与平面的法向量,代入公式即可

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
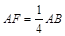 .
.
 中,底面
中,底面 是矩形,
是矩形,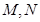 分别为
分别为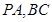 的中点,
的中点,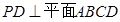 ,且
,且
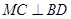 ;
; 的余弦值。
的余弦值。 为正方形
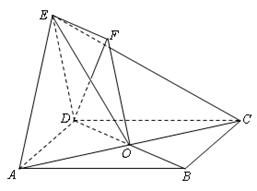
为正方形 的中心,四边形
的中心,四边形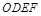 是平行四边形,且平面
是平行四边形,且平面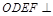 平面
平面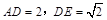 .
.
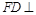 平面
平面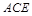 .
.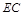 上是否存在一点
上是否存在一点 ,使
,使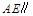 平面
平面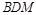 ?若存在,求
?若存在,求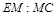 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.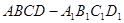 中,面
中,面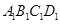 中心为
中心为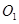 .
.
 面
面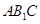 ;
;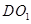 与
与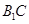 所成角.
所成角.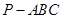 中,
中,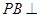 底面
底面 于
于 ,
, ,
, ,点
,点 是
是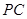 的中点.
的中点.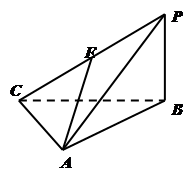
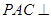 平面
平面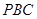 ;
;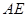 与
与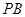 所成的角为
所成的角为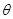 ,且
,且 ,
,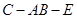 的大小.
的大小.  .证明:平面PAD⊥平面PDC.
.证明:平面PAD⊥平面PDC.
 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点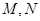 分别为
分别为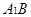 和
和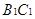 的中点.
的中点.
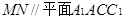 ;
; 的正弦值.
的正弦值.
 的距离.
的距离.